
Mein Einstieg in die Kryptowelt - Explorative Datenanalyse
- 73 mins- Einleitung
- Wieso wurde es eigentlich die Kryptowelt?
- Wissenschaftliches Ziel
- Datenbeschaffung
- Erste Analyse
- Linienchart vs Candlechart
- Kryptowährung Korrelationsanalyse
- Zeitreihendekomposition Ripple
- Ich habe mich entschieden
- Wo wird das meiste Kapital bewegt?
- Was macht unser Invest?
- Wir träumen kurz
- Den Ripple-Wert prognostizieren!
Einleitung
In diesem Skript möchte ich über meinen Einstieg in die Kryptowelt berichten. Initial werde ich darüber schreiben wieso ich eigentlich den doch recht volatilen Kryptomarkt ausgewählt habe um eine Investition zu tätigen. Darüber hinaus werden wir kurz in die Welt der Chartanalyse einsteigen, wo wir mehr über die Candlestickchart Analyse erfahren werden und wieso man Candlstick-Charts ganz klar tristen und langweiligen Liniencharts vorziehen sollte. Es wird unter anderem eine Korrelationsmatrix der ausgewählten Kryptowährungen erstellt um Korrelationen zwischen den jeweiligen Währungen zu erfassen bzw. den Grad des Zusammenhangs zwischen diesen Währungen. Dazu werde ich mich auf einige anschauliche Datenvisualisierungen konzentrieren. Anschließend werde ich eine Zeitreihendekomposition auf eine von mir ausgewählte Währung durchführen, mit dem Ziel herauszufinden ob es z.B. einen Trend oder Saisonalität in den Daten gibt. Nach der Zerlegung der Zeitreihe werde ich euch zeigen wie meine erste Investition abgelaufen ist. Während der Wartezeit werden wir uns mit der Fragestellung “Wo wird das meiste Kapital bewegt?” beschäftigen und uns für die Beantwortung dieser Frage historische Exchange- (Börsen) Daten besorgen und diese analysieren. Im Anschluß werden wir uns mal anschauen wie sich unser Invest so entwickelt und uns kurz in ein “was-wäre-wenn”-Szenario eindenken. Danach kommen wir auch schon zum Ende, wo wir anhand von Machine Learning Algorithmen versuchen werden den Ripple-Wert zu prognostizieren.
Warum wurde es eigentlich die Kryptowelt?
Das Ganze begann am 18.Dezember 2017. Bis zu diesem Zeitpunkt habe ich mir öfters darüber Gedanken gemacht, wie ich eigentlich einen Teil meiner Ersparnisse (500€) in etwas investieren möchte. Das ich das tun möchte war klar, aber wohin war die Frage? Die Kryptowelt habe ich bis zu diesem Zeitpunkt schon länger im Auge gehabt, jedoch habe ich nie ernsthafte Gedanken darüber verschwendet mal etwas Geld darein zu stecken, bis mir ein sehr guter Freund davon erzählt hat, dass er in nur zwei Monaten aus 10.000€ dank der Investition in Kryptowährungen knapp 70.000€ erwirtschaftet hat. Das Ganze hat mich sehr fasziniert, also habe ich den Schritt gewagt und mich in die Thematik eingearbeitet.
Durch erste intensive Recherchen bin ich zum Entschluss gekommen in die Kryptowelt zu investieren, da diese noch recht am Anfang steht. Man hat also die Möglichkeit mit noch niedrigen Preisen in etwas Zukunftsträchtiges zu investieren. Ich bin mir darüber bewusst, dass das ganze hochvolatil ist und eher einem Lottospiel ähnelt. Trotzdem wollte ich das Risiko eingehen und ein Experiment starten.
Kryptowährungen sind dezentral und demokratisch organisiert. Damit ist das nahe zu fälschungssicher und durch keine Notenbank kontrolliert. Die maximale Anzahl von Kryptowährungen sind beschränkt. – Nicht wie bei unseren Notenbanken, die rein theoretisch einfach Geld drucken können, wann sie wollen.
Die Technologie hinter Kryptowährungen wird meiner Meinung nach die Welt verändern. Sie speichern alle Informationen in einem sogenannten digitalen Logbuch. Alle beteiligten Personen bestätigen jede eingehende Information. Es entsteht quasi ein gemeinsamer Konsens, eine demokratische Währung.
Natürlich kann ich auch in Aktien o.ä. investieren, aber wegen 500€ gehe ich nicht zu einem Anlagenberater. Die Einstiegshürde bei Kryptowährungen ist meiner Meinung nach einfach niedriger. Das Ganze ist nicht kompliziert:
- Man meldet sich bei einer Börse an
- Um bei einer Börse Geld einzuzahlen, muss man sich zuerst verifizieren. Solche Börsen müssen diese Daten von mir verlangen, zum einen um Geldwäsche zu verhindern und zum anderen wegen der Know-Your-Customer Regelung.
- Geld über eine SEPA Überweisung einzahlen
- Mit sogenanntem Fiatgeld (€) kann man sich nun Kryptowährungen einkaufen.
Ich habe mich am 20. Dezember bei einer Börse registriert (Bitstamp) und die Verifizierungsunterlagen eingereicht. Schon am 21. Dezember ist die Bestätigung über meine erfolgreiche Verifizierung in mein E-Mail-Postfach eingetrudelt. Am selbigen Tag habe ich das Geld überwiesen, da das ganze jedoch eine Auslandsüberweisung war, ist die Einzahlungsbestätigung zwei Tage später endlich eingetroffen.
Ich konnte also endlich beginnen in Kryptowährungen zu investieren. Bevor ich das jedoch tat, musste ich natürlich erstmal Schauen in welche der unzähligen Währungen ich investieren werden.
Auf http://www.coinmarketcap.com kann man eine Übersicht, der aktuell offiziell gelisteten Kryptowährungen und ihre jeweilige Marktkapitalisierung finden.
Wissenschaftliches Ziel
Das Wissenschaftliche Ziel dieser Arbeit besteht nicht nur aus einem Ziel, sondern aus drei Fragestellungen:
-
Kann mir eine statistische Analyse der historischen Kryptowährung zum Reichtum helfen? Dazu werden wir unter anderem Deskriptive Analysen durchführen um die Erkenntnisse auf die Zukunft anzuwenden.
-
Kann man den Preis einer Kryptowährung anhand von Machine Learning Algorithmen vorhersagen?
-
Wo wird am meisten Kapital bewegt?
Mich interessieren folgende Kryptowährungen:
- Bitcoin
- Ethereum
- Ripple
- IOTA
- Monero
- NEO
- DASH
- Litecoin
Datenbeschaffung
Zunächst einmal benötigen wir Daten. Das heißt für uns: Historische Kryptowährungkurse über einen etwas längeren Zeitraum um o.g. Fragestellungen zu beantworten.
Die von mir oben genannten Währungen befinden sich alle in der Top 15 (nach Marktkapitalisierung). Zusätzlich sind die vorgestellten Technologien ziemlich interessant.
Es wird eine Daten-Pull Funktion definiert, welche von der o.g. Website für die in einer Liste angegebenen Kryptowährungen die historischen Daten lokal in eine .csv Datei einspeichert:
import re
import sys
import csv
import time
import random
import requests
from datetime import date
from bs4 import BeautifulSoup
import warnings
warnings.filterwarnings('ignore')
end_date = str(date.today()).replace("-","")
base_url = "https://coinmarketcap.com/currencies/{0}/historical-data/?start=20130501&end="+end_date #Frühestes Datum: 01.05.2013...
currency_name_list = ["bitcoin", "ethereum", "ripple","iota","monero","neo","dash","litecoin"]
def get_data(currency_name):
print("Währung : ", currency_name)
url = base_url.format(currency_name)
html_response = requests.get(url).text.encode('utf-8')
soup = BeautifulSoup(html_response, 'html.parser')
table = soup.find_all('table')[0]
elements = table.find_all("tr")
with open("datas/{0}_preise.csv".format(currency_name.replace("-","_")),"w") as ofile:
writer = csv.writer(ofile)
for element in elements:
writer.writerow( element.get_text().strip().split("\n") )
time.sleep(1)
if __name__ == "__main__":
print("Lade Historische Daten runter...")
for currency_name in currency_name_list:
get_data(currency_name)
pass
print("Fertig")
Lade Historische Daten runter...
Währung : bitcoin
Währung : ethereum
Währung : ripple
Währung : iota
Währung : monero
Währung : neo
Währung : dash
Währung : litecoin
Fertig
Schauen wir uns doch mal den Datensatz der wohl berühmtesten Kryptowährung an, dem Bitcoin:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import matplotlib.style as style
from pylab import rcParams
style.available
%matplotlib inline
import seaborn as sns
color = sns.color_palette()
style.use('fivethirtyeight')
df_bitcoin = pd.read_csv("data/bitcoin_preise.csv", parse_dates=['Date'])
df_bitcoin.head()
| Date | Open | High | Low | Close | Volume | Market Cap | |
|---|---|---|---|---|---|---|---|
| 0 | 2017-12-28 | 15864.1 | 15888.4 | 13937.3 | 14606.5 | 12,336,500,000 | 265,988,000,000 |
| 1 | 2017-12-27 | 16163.5 | 16930.9 | 15114.3 | 15838.5 | 12,487,600,000 | 270,976,000,000 |
| 2 | 2017-12-26 | 14036.6 | 16461.2 | 14028.9 | 16099.8 | 13,454,300,000 | 235,294,000,000 |
| 3 | 2017-12-25 | 13995.9 | 14593.0 | 13448.9 | 14026.6 | 10,664,700,000 | 234,590,000,000 |
| 4 | 2017-12-24 | 14608.2 | 14626.0 | 12747.7 | 13925.8 | 11,572,300,000 | 244,824,000,000 |
Was sehen wir?
- Date: Gibt das Datum an, für die die weiteren Werte gelten.
- Open: Der Eröffnungspreis für den in ‘Date’ angegebenen Tag.
- High: Der Höchstkurs für den in ‘Date’ angegebenen Tag.
- Low: Der Tiefstkurs für den in ‘Date’ angegebenen Tag.
- Close: Der Schlusskurs für den in ‘Date’ angegebenen Tag.
- Volume: Das Volumen für den in ‘Date’ angegebenen Tag, also was in den 24 Stunden gehandelt wurde.
- Market Cap: Die Marktkapitalisierung.
Die Marktkapitalisierung ergibt sich aus dem Produkt von dem aktuellen Preis und der Menge an Währungen die im Umlauf sind.
Marktkapitalisierung = Anzahl der in Umlauf befindlichen Coins × Börsenkurs je Coin
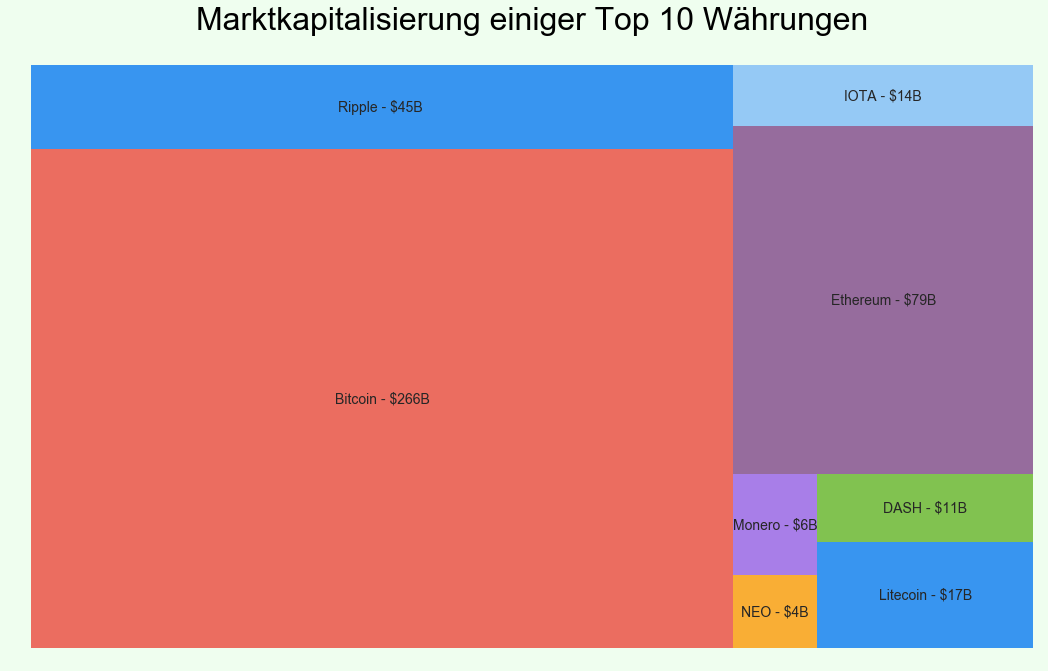
In der unteren Grafik ist zu erkennen, dass der Bitcoin ganz klar den Markt mit seinen $266 Milliarden (Stand 22.12.2017) Marktkapitalisierung dominiert.
import squarify
import datetime
marketcap = pd.read_csv("data/marketcap_22122017.csv")
style.use('fivethirtyeight')
fig, ax = plt.subplots(figsize=(16,10))
colors = ["#248af1", "#eb5d50", "#8bc4f6", "#8c5c94", "#a170e8", "#fba521", "#75bc3f"]
# Plot
squarify.plot(sizes=marketcap["Market Cap"], label=marketcap["Cryptocurrency"], alpha=0.9, color=colors)
plt.axis('off')
plt.gca().invert_yaxis()
plt.title("Marktkapitalisierung einiger Top 10 Währungen", fontsize=32, color="Black")
ttl = ax.title
ttl.set_position([.5, 1.05])
fig.set_facecolor('#effeef')
Erste Analysen
Nun lassen wir uns doch mal den Gaphen zum Schlusskurs des Bitcoins plotten. Ich möchte gerne sehen, wie sich eigentlich der Bitcoin so über die Zeit entwickelt hat.
import matplotlib.dates as mdates
df_bitcoin = df_bitcoin[df_bitcoin['Date'] < '2017-12-22']
df_bitcoin['Date_mpl'] = df_bitcoin['Date'].apply(lambda x: mdates.date2num(x))
fig, ax = plt.subplots(figsize=(12,8))
sns.tsplot(df_bitcoin.Close.values, time=df_bitcoin.Date_mpl.values, alpha=0.8, color=color[3], ax=ax)
ax.xaxis.set_major_locator(mdates.AutoDateLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y.%m.%d'))
fig.autofmt_xdate()
plt.xlabel('Datum', fontsize=12)
plt.ylabel('Preis in USD', fontsize=12)
plt.title("Schlusskurs Preis Verteilung von Bitcoin", fontsize=15)
plt.show()
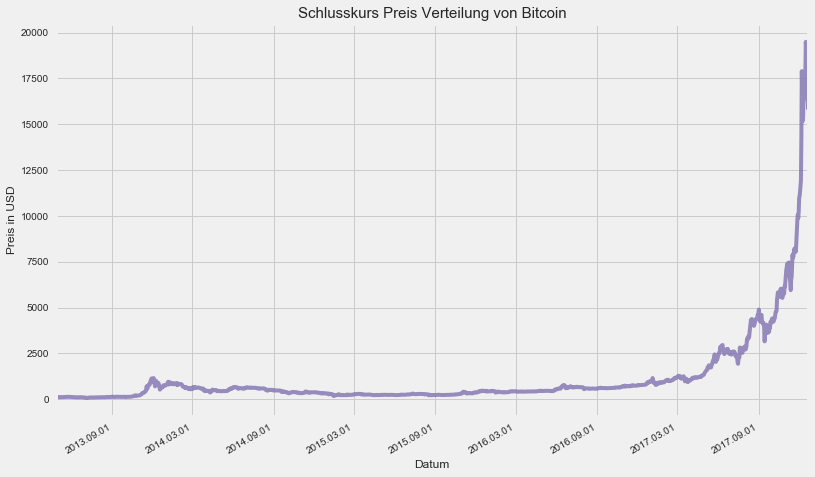
Wir sehen der Bitcoin hat im Jahr 2017 eine ziemlich gute Entwicklung gemacht. Bis 2017 sah alles noch recht nett aus, aber dann ab ca. Oktober 2017 könnte man meinen, oh die Achse ist völlig überbewertet und durch die Decke gegangen, d.h. hier würde ich jetzt sagen, dass ich auf gar keinen Fall mehr einsteigen möchte. Optisch hätte mir der Verlauf bis zum Oktober 2017 schon eher zugesagt bzw. ich hätte das ganze als einen vernünftigen Anstieg bewertet.
Deswegen schauen wir uns jetzt mal das ganze in einer logarithmischen Skalierung an um besser nachvollziehen zu können, was eigentlich passiert ist und sich somit nicht von optischen Übertreibungen aufgrund der linearen Skalierung durcheinander bringen lassen zu wollen.
fig, ax = plt.subplots(figsize=(12,8))
ax.set_xscale('log')
ax.set_yscale('log')
sns.tsplot(df_bitcoin.Close.values, time=df_bitcoin.Date_mpl.values, alpha=0.8, color=color[3], ax=ax)
ax.xaxis.set_major_locator(mdates.AutoDateLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y.%m.%d'))
fig.autofmt_xdate()
plt.xlabel('Datum', fontsize=12)
plt.ylabel('Preis in USD', fontsize=12)
plt.title("Schlusskurs Preis Verteilung von Bitcoin - logarithmisch", fontsize=15)
plt.show()
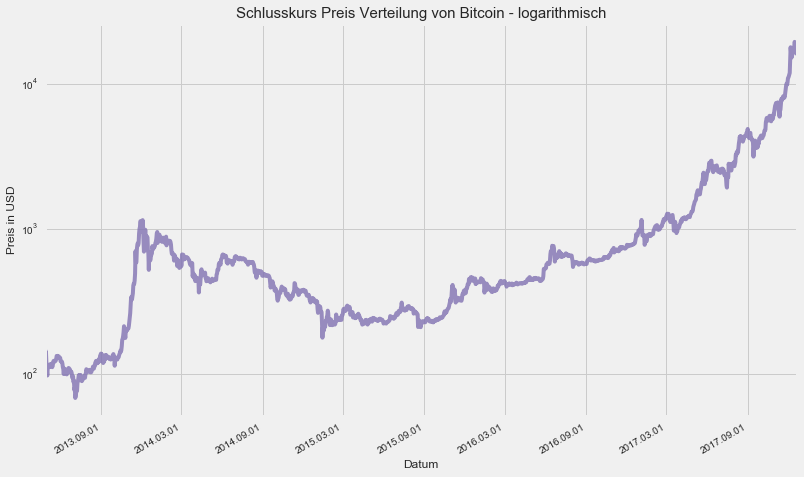
Schon viel besser.
Linienchart vs Candlestick Chart
Nun haben wir eine Art der Visualisuerung von Kursen gesehen. Doch mich haben die Liniencharts nicht zufrieden gestellt, denn diese zeigen mir nur die Schlusskurse eines Tages an. Durch eine Recherche bin ich auf die Candlecharts gestoßen.
Ein Linienchart wie oben zeigt uns also nur die Schlusskurse an, während Candlecharts folgendes beinhalten:
- Eröffnunfskurs
- Schlussskurs
- Höchstkurs
- Tiefstkurs
eines bestimmten zeitintervalls. (Hier 24Std)
Aufbau Candlechart:
- Oberer Docht (oder manchmal auch oberer Schatten genannt)
- Körper
- Unterer Docht (oder manchmal auch unterer Schatten genannt)
Grüne Farbe = Wird Grün gezeichnet wenn der Kurs in der Zeit in der er sich geformt hat, gestiegen ist.
- unteres Ende des Körpers zeigt den Eröffungskurs
- oberes Ende des Körpers zeigt den Schlusskurs
Rote Farbe = Wird Grün gezeichnet wenn der Kurs in der Zeit in der er sich geformt hat, gesunken ist.
- unteres Ende des Körpers zeigt den Schlusskurs
- oberes Ende des Körpers zeigt den Eröffnungskurs
Die Dochte zeigen den Höchstkurs und Tiefskurs an
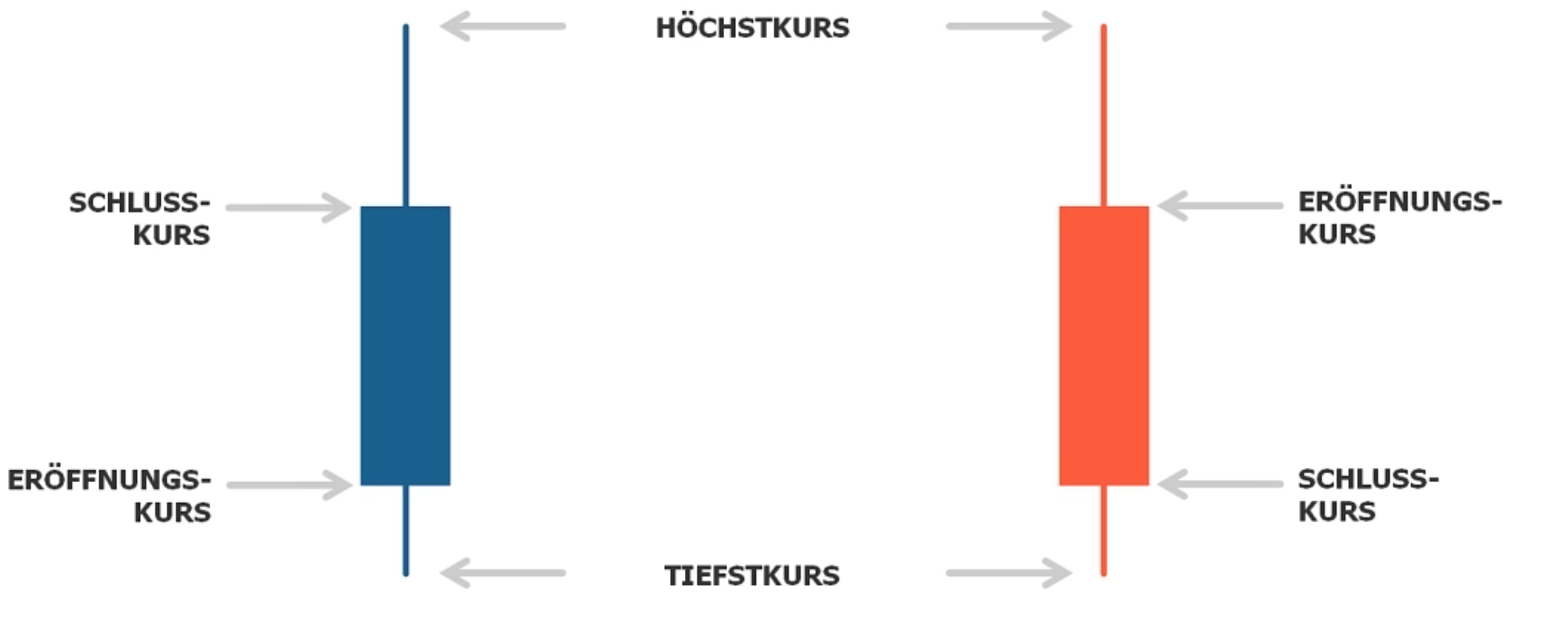
Aufsteigender Kurs wird als BULLISH bezeichnet:
Fallender Kurs wird BEARISH genannt:
Wie lese ich sie?
Lange Dochte zeigen Änderungen der Marktstimmung an.
Je länger die Dochte eines fertig geformten Candlesticks, desto größer war die Änderung der Marktstimmung wärend sich der Candlestick geformt hat
Der Doji
Wenn das Verhätlnis zwischen Käufer und Verkäufer ausgewogen ist, bildet sich ein “Doji”

Charakteristik: Der Verhältnis zu den Dochten sehr kleine Körper.
Ein sehr kurzer Körper zeigt das ausgewogene Verhältnis zwischen Bullen und Bären
–> Also Gleichgewicht zwischen Käufer und Verkäufer
Wenn sich ein Doji bildet, ist das ein Zeichen von unentschlossenheit im Markt.
Je größer ein bullisher Candlestick Körper im Verhältnis zu den Dochten, umso stärker kontrollieren Käufer den Markt.
Je größer ein bearisher Candlestick Körper im erältnis zu den Dochten, umso stärker kontrollieren Verkäufer den Markt
Um mehr über Candlestick Charts und Chartanalyse Techniken zu Erfahren empfehle ich folgendes:
- https://www.youtube.com/watch?v=OGFxp3Pixg8
Schauen wir uns nun doch mal solch einen Candlestick Chart an. Die matplotlib Bibliothek liefert uns eine Möglichkeit diese zu plotten:
import matplotlib.ticker as mticker
from matplotlib.finance import candlestick_ohlc
fig = plt.figure(figsize=(20,10))
ax1 = plt.subplot2grid((1,1), (0,0))
temp_df = df_bitcoin[df_bitcoin['Date'] >='2017-10-01']
ohlc = []
for ind, row in temp_df.iterrows():
ol = [row['Date_mpl'],row['Open'], row['High'], row['Low'], row['Close'], row['Volume']]
ohlc.append(ol)
candlestick_ohlc(ax1, ohlc, width=0.4, colorup='#77d879', colordown='#db3f3f')
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d'))
ax1.xaxis.set_major_locator(mticker.MaxNLocator(10))
plt.xlabel("Datum", fontsize=12)
plt.ylabel("Preis in USD", fontsize=12)
plt.title("Candlestick chart für Bitcoin", fontsize=15)
plt.subplots_adjust(left=0.09, bottom=0.20, right=0.94, top=0.90, wspace=0.2, hspace=0)
plt.show()
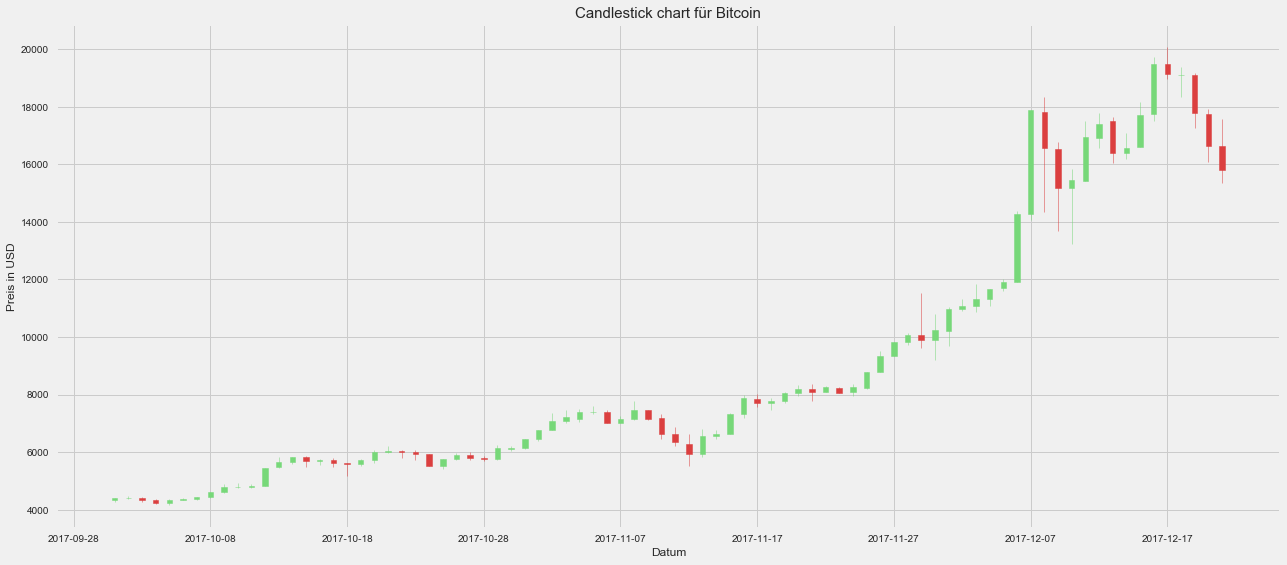
Kryptowährung Korrelationsanalyse
Nun haben wir gelernt wie Candlestickcharts im Allgemeinen funktionieren. Gehen wir einen Schritt weiter. Ziel dieser Analyse ist es eine Korrelationsmatrix für die oben gelisteten Währungen zu erzeugen. Ich möchte damit u.a. prüfen, ob die von mir genannten Währungen untereinander abhängig sind. Ich liebäugle derzeit mit der Währung Ripple, hier sagt mir das ganze Konzept zu, außerdem wird die Technologie schon eingesetzt; das Proof-of-concept ist somit durch und das ganze ist nicht mehr so spekulativ. Mir wäre unabhängigkeit wichtig. Mal schauen was die Korrelationsanalyse hier ausspuckt.
Bevor die Korrelation berechnet wird, ist es wichtig, stationäre Daten zu haben. Es gibt einige Möglichkeiten, Daten stationär zu machen - eine davon durch Differenzierung. Aber auch danach ist es schwierig, falsche Korrelationen zwischen Zeitreihen zu vermeiden, die oft durch Autokorrelation verursacht werden. Korrelationen zwischen nichtstationären sind oft falsch und repräsentieren keine tatsächliche Korrelation zwischen den Datensätzen. Eine detaillierte Erklärung hierzu findet man in diesem Artikel:
- http://www.math.ku.dk/~sjo/papers/LisbonPaper.pdf.
Was bedeutet eigentlich Stationarität für unsere Daten?
In der Zeitreihenanalyse und -modellierung möchten wir immer, dass Daten stationär sind. Es gibt mehrere komplexe mathematische Definitionen von Stationarität, aber in einfachen Begriffen hat eine stationäre Zeitreihe keinen Aufwärts- oder Abwärtstrend über die Zeit und die Varianz der Zeitreihe ist über die Zeit stabil.
Hier ist ein Beispiel. Die obige Serie scheint eine Varianz zu haben, die über die Zeit stabil ist, aber einen Aufwärtstrend aufweist. Diese Reihe ist nicht stationär. Die untere Reihe ist der Unterschied der obersten Reihe. Es ist stationär, weil der Mittelwert über die Zeit gleich bleibt. Es hat keinen Trend.

Diese Serie ist nicht stationär. Es hat einen Aufwärtstrend und die Varianz nimmt mit der Zeit ebenfalls zu.
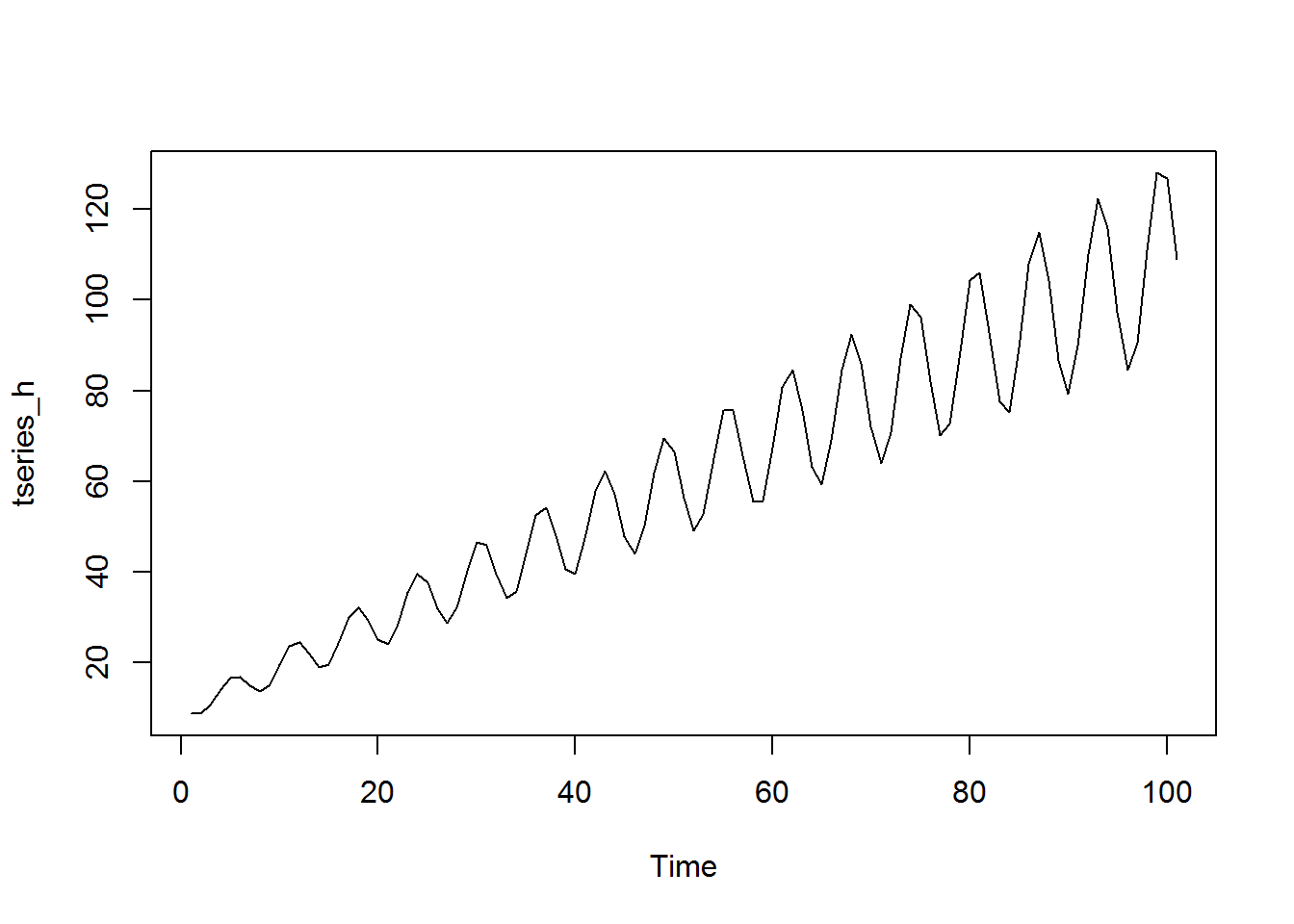
Denken wir mal daran, die Korrelation von zwei Serien (z.B. verschiedene Kryptowährungen) zu nehmen, die beide im Zeitverlauf nach oben verlaufen. Wir würden eine starke Korrelation bekommen, aber dies nur, weil die Reihe mit der Zeit zunimmt, nicht weil die Bewegung in der einen mit der Bewegung in der anderen verbunden ist. Dies ist eine falsche Korrelation.
Um die Korrelation zweier Zeitreihen zu erfassen, möchten wir diese zunächst stationär machen (z. B. durch Differenzbildung). Oft (aber nicht immer) wird eine starke Korrelation zwischen zwei nichtstationären Zeitreihen nach der Differenzierung verschwinden.
Zunächst findet eine schnelle Datenreinigung statt…
crypto = {}
crypto['bitcoin'] = pd.read_csv('data/bitcoin_preise.csv')
crypto['dash'] = pd.read_csv("data/dash_preise.csv")
crypto['ethereum'] = pd.read_csv("data/ethereum_preise.csv")
crypto['iota'] = pd.read_csv("data/iota_preise.csv")
crypto['litecoin'] = pd.read_csv("data/litecoin_preise.csv")
crypto['monero'] = pd.read_csv("data/monero_preise.csv")
crypto['neo'] = pd.read_csv("data/neo_preise.csv")
crypto['ripple'] = pd.read_csv("data/ripple_preise.csv")
#Wir schauen uns nur die Schlusskurse an um das ganze besser handlen zu können
for coin in crypto:
for column in crypto[coin].columns:
if column not in ['Date', 'Close']:
crypto[coin] = crypto[coin].drop(column, 1)
# das Datum als Datetime-Typ und reindex
crypto[coin]['Date'] = pd.to_datetime(crypto[coin]['Date'])
crypto[coin] = crypto[coin].sort_values('Date')
crypto[coin] = crypto[coin].set_index(crypto[coin]['Date'])
crypto[coin] = crypto[coin].drop('Date', 1)
for coin in crypto:
print(coin, len(crypto[coin]))
bitcoin 1706
dash 1414
ethereum 875
iota 199
litecoin 1706
monero 1317
neo 476
ripple 1608
#schmeissen wir mal iota raus...da recht junger coin und es noch nicht viele datenpunkte gibt.
# Für die restlichen Währungen werde ich nur die letzten 400 Datenpunkte betrachten
del crypto['iota']
cryptoAll = {} # für später...
for coin in crypto:
cryptoAll[coin] = crypto[coin]
crypto[coin] = crypto[coin][-400:]
for coin in crypto:
print(coin, len(crypto[coin]))
bitcoin 400
dash 400
ethereum 400
litecoin 400
monero 400
neo 400
ripple 400
Wir werden jetzt erstmal nur die tägliche Differenz betrachten, da diese nicht saisonabhängig ist. Wir transformieren unsere Zeitreihe also wie folgt:
data[t] = data[t] - data[t-1].
Auf dieser Datenbasis werden wir die Stationarität testen um uns letzendlich auf die Korrelationstests vorzubereiten:
# Differenzierung...
for coin in crypto:
crypto[coin]['AbschlUnt'] = crypto[coin]['Close'].diff().fillna(0)
Grafische Darstellung
schauen wir uns mal die Grafik an…
for coin in crypto:
plt.plot(crypto[coin]['AbschlUnt'], label=coin)
plt.legend(loc=2)
plt.title('Tägliche Differenzierte Schlusskurse')
plt.show()
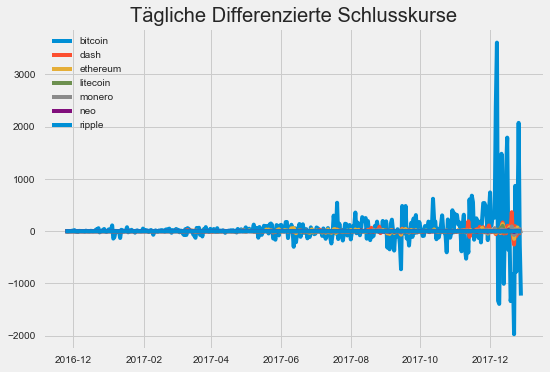
Info:
Wir sehen, dass das Einführen der täglichen differenz der Schlusskurve uns wohlmöglich schon eine Stationarität in den Daten gegeben hat. Außerdem sehen wir, dass eine der Währung (Bitcoin) viel größere Spitzen als die anderen Währungen hat. Es könnte nützlich sein, auch die prozentuale Veränderung pro Tag der Zeitreihen zu betrachten.
# Prozentuale Änderung
for coin in crypto:
crypto[coin]['ProzAend'] = crypto[coin]['Close'].pct_change().fillna(0)
fig = plt.figure(figsize=(12,8))
for coin in crypto:
plt.plot(crypto[coin]['ProzAend'], label=coin)
plt.legend(loc=2)
plt.title('Tägliche prozentuale Veränderung des Schlusskurses')
plt.show()
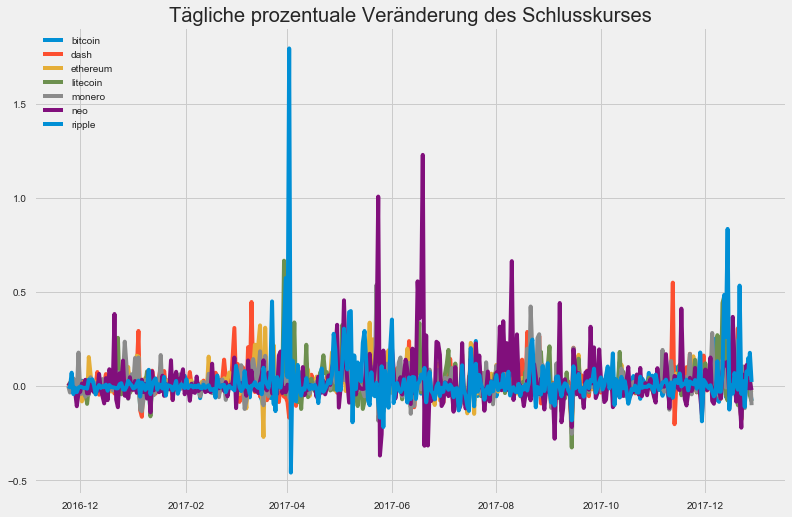
Notiz:
Wie zuvor haben wir immer noch sehr große Peaks, aber die Daten sehen insgesamt besser aus als zuvor. Vor allem haben wir keine Währung, die die anderen dominiert.
Konzentrieren wir uns auf einen bestimmten Teil des Diagramms, um eine Vorstellung von einer Korrelation zu erhalten.
fig = plt.figure(figsize=(12,8))
for coin in crypto:
plt.plot(crypto[coin]['ProzAend'][-20:], label=coin)
plt.legend(loc=2)
plt.title('Tägliche prozentuale Veränderung des Schlusskurses')
plt.show()
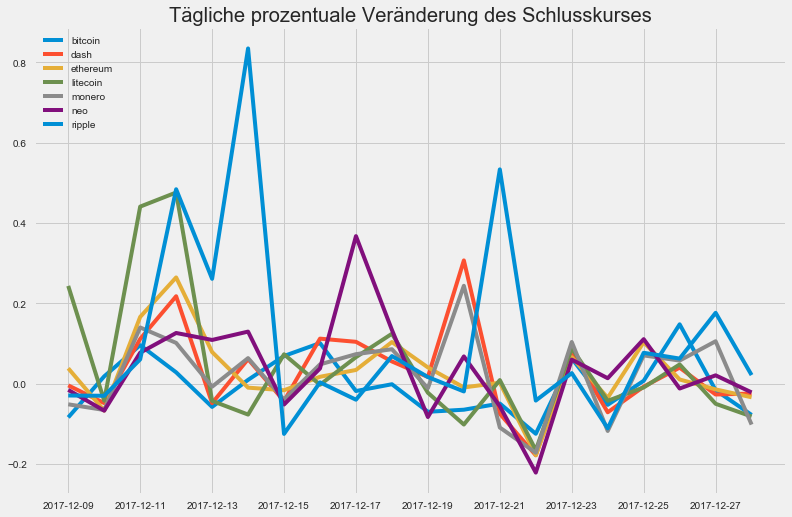
Info:
Sieht zumindest schonmal so aus, als hätten wir tatsächlich eine Korrelation…
Stationarität prüfen
Um spätere Werte zu verstehen, kommen wir leider nicht um die Theorie des Verfahrens zur Stationaritätsprüfung drumherum.
Der Augmented Dickey-Fuller-Test ist eine Art von statistischem Test, der als Einheitswurzeltest bezeichnet wird. Die Intuition hinter einem Unit-Root-Test ist, dass er bestimmt, wie stark eine Zeitreihe durch einen Trend definiert ist.
Es gibt eine Anzahl von Einheitswurzeltests und der Augmented Dickey-Fuller ist einer der am weitesten verbreiteten. Es verwendet ein autoregressives Modell und optimiert ein Informationskriterium über mehrere verschiedene Verzögerungs-Werte (auch genannt Lag-Werte) hinweg.
Die Nullhypothese des Tests ist, dass die Zeitreihe durch eine Einheitswurzel dargestellt werden kann, dass sie nicht stationär ist (hat eine zeitabhängige Struktur). Die alternative Hypothese (Ablehnung der Nullhypothese) ist, dass die Zeitreihe stationär ist.
-
Nullhypothese (H0): Wenn sie akzeptiert wird, schlägt sie vor, dass die Zeitreihe eine Einheitswurzel hat, was bedeutet, dass sie nicht stationär ist. Es hat eine zeitabhängige Struktur.
-
Alternativhypothese (H1): Die Nullhypothese wird abgelehnt; es deutet darauf hin, dass die Zeitreihe keine Einheitswurzel hat, d.h. sie ist stationär. Es hat keine zeitabhängige Struktur.
Wir interpretieren dieses Ergebnis mit dem p-Wert aus dem Test. Ein p-Wert unter einem Schwellenwert (wie 5% oder 1%) deutet darauf hin, dass wir die Nullhypothese (stationär) ablehnen, da andernfalls ein p-Wert über dem Schwellenwert die Annahme der Nullhypothese (nicht stationär) nahelegt.
-
p-Wert > 0,05: Akzeptiere die Nullhypothese (H0), die Daten haben eine Einheitswurzel und sind nicht stationär.
-
p-Wert <= 0.05: Verwerfen die Nullhypothese (H0), die Daten haben keine Einheitswurzel und sind stationär.
Weitere Details über das Verfahren des Testens auf Stationarität univariater Zeitreihen finden sich auf:
- https://www.uni-marburg.de/fb02/statistik/studium/vorl/zroeko/tsunitroots.pdf
from statsmodels.tsa.stattools import acf, adfuller
for coin in crypto:
print('\n',coin)
adf = adfuller(crypto[coin]['ProzAend'][1:])
print(coin, 'ADF Statistik: %f' % adf[0])
print(coin, 'P-Wert: %f' % adf[1])
print(coin, 'Kritische Werte', adf[4]['1%'])
print(adf)
bitcoin
bitcoin ADF Statistik: -18.952851
bitcoin P-Wert: 0.000000
bitcoin Kritische Werte -3.4468876315
(-18.95285054857678, 0.0, 0, 398, {'1%': -3.4468876315017423, '5%': -2.8688294245285162, '10%': -2.5706530597712178}, -1222.5822949255294)
dash
dash ADF Statistik: -20.802974
dash P-Wert: 0.000000
dash Kritische Werte -3.4468876315
(-20.802973522823912, 0.0, 0, 398, {'1%': -3.4468876315017423, '5%': -2.8688294245285162, '10%': -2.5706530597712178}, -842.85058764270934)
ethereum
ethereum ADF Statistik: -19.136047
ethereum P-Wert: 0.000000
ethereum Kritische Werte -3.4468876315
(-19.136046896833982, 0.0, 0, 398, {'1%': -3.4468876315017423, '5%': -2.8688294245285162, '10%': -2.5706530597712178}, -922.04304395048621)
litecoin
litecoin ADF Statistik: -18.810916
litecoin P-Wert: 0.000000
litecoin Kritische Werte -3.4468876315
(-18.810916317936144, 2.0224428720868981e-30, 0, 398, {'1%': -3.4468876315017423, '5%': -2.8688294245285162, '10%': -2.5706530597712178}, -787.44296126916015)
monero
monero ADF Statistik: -21.433191
monero P-Wert: 0.000000
monero Kritische Werte -3.4468876315
(-21.433190781562587, 0.0, 0, 398, {'1%': -3.4468876315017423, '5%': -2.8688294245285162, '10%': -2.5706530597712178}, -847.55391401015231)
neo
neo ADF Statistik: -12.737365
neo P-Wert: 0.000000
neo Kritische Werte -3.44692956197
(-12.737365193179572, 9.0995811321685848e-24, 1, 397, {'1%': -3.4469295619737665, '5%': -2.8688478565083417, '10%': -2.570662885558566}, -415.54259858216972)
ripple
ripple ADF Statistik: -9.150585
ripple P-Wert: 0.000000
ripple Kritische Werte -3.44697170562
(-9.1505849091476481, 2.693345362338313e-15, 2, 396, {'1%': -3.4469717056192213, '5%': -2.868866381945153, '10%': -2.5706727611978368}, -439.83005918192964)
for coin in crypto:
print('\n',coin)
adf = adfuller(crypto[coin]['AbschlUnt'][1:]) #das selbe für den
print(coin, 'ADF Statistik: %f' % adf[0])
print(coin, 'P-Wert: %f' % adf[1])
print(coin, 'Kritische Werte', adf[4]['1%'])
print(adf)
bitcoin
bitcoin ADF Statistik: -5.454369
bitcoin P-Wert: 0.000003
bitcoin Kritische Werte -3.44758504386
(-5.4543694596922832, 2.6015317532110729e-06, 16, 382, {'1%': -3.4475850438570115, '5%': -2.8691359637671252, '10%': -2.5708164748773332}, 5493.0720065394489)
dash
dash ADF Statistik: -2.870378
dash P-Wert: 0.048903
dash Kritische Werte -3.44763059042
(-2.8703777808311433, 0.048902687459284007, 17, 381, {'1%': -3.4476305904172904, '5%': -2.8691559808203548, '10%': -2.5708271462031811}, 3707.4495616915433)
ethereum
ethereum ADF Statistik: -3.393146
ethereum P-Wert: 0.011195
ethereum Kritische Werte -3.44763059042
(-3.3931464493637749, 0.011194739313798085, 17, 381, {'1%': -3.4476305904172904, '5%': -2.8691559808203548, '10%': -2.5708271462031811}, 3298.4999922713655)
litecoin
litecoin ADF Statistik: -3.466386
litecoin P-Wert: 0.008894
litecoin Kritische Werte -3.44763059042
(-3.4663857412607046, 0.0088935295876547728, 17, 381, {'1%': -3.4476305904172904, '5%': -2.8691559808203548, '10%': -2.5708271462031811}, 2598.1440273967323)
monero
monero ADF Statistik: -2.888564
monero P-Wert: 0.046694
monero Kritische Werte -3.44763059042
(-2.8885639304273609, 0.046694110298213451, 17, 381, {'1%': -3.4476305904172904, '5%': -2.8691559808203548, '10%': -2.5708271462031811}, 2755.8066689053171)
neo
neo ADF Statistik: -10.943252
neo P-Wert: 0.000000
neo Kritische Werte -3.44697170562
(-10.943251846882063, 9.182216194014438e-20, 2, 396, {'1%': -3.4469717056192213, '5%': -2.868866381945153, '10%': -2.5706727611978368}, 1760.8195114705948)
ripple
ripple ADF Statistik: -0.511688
ripple P-Wert: 0.889715
ripple Kritische Werte -3.44753973677
(-0.51168849629182778, 0.88971531115306934, 15, 383, {'1%': -3.4475397367687202, '5%': -2.8691160516676844, '10%': -2.5708058595395702}, -1533.555161088319)
Wir sehen, die p-Werte sind alle extrem niedrig. Somit sind die Daten stationär! Es war also eine gute Idee auf die differenzierten Tageswerte oder die prozentuale Veränderung zu setzen.
Korrelationen
Jetzt werden wir die Korrelation zwischen den verschiedenen Währungen betrachten.
corrDF_n = pd.DataFrame()
for coin in crypto:
corrDF_n[coin] = crypto[coin]['ProzAend']
plt.matshow(corrDF_n.corr(method='pearson'))
plt.xticks(range(8), corrDF_n.columns.values, rotation='vertical')
plt.yticks(range(8), corrDF_n.columns.values)
plt.xlabel('Pearson Korrelation')
plt.show()
corrDF_n.corr(method='pearson')
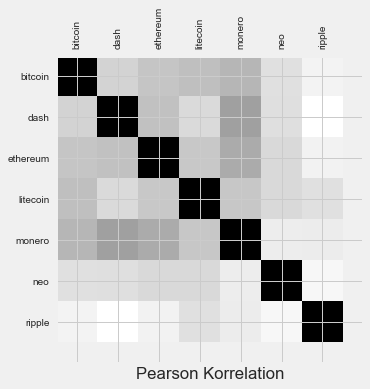
| bitcoin | dash | ethereum | litecoin | monero | neo | ripple | |
|---|---|---|---|---|---|---|---|
| bitcoin | 1.000000 | 0.282338 | 0.341977 | 0.369511 | 0.400287 | 0.214793 | 0.105382 |
| dash | 0.282338 | 1.000000 | 0.362552 | 0.249198 | 0.469864 | 0.223029 | 0.008049 |
| ethereum | 0.341977 | 0.362552 | 1.000000 | 0.329353 | 0.434373 | 0.255004 | 0.115747 |
| litecoin | 0.369511 | 0.249198 | 0.329353 | 1.000000 | 0.336975 | 0.254737 | 0.216995 |
| monero | 0.400287 | 0.469864 | 0.434373 | 0.336975 | 1.000000 | 0.144276 | 0.152624 |
| neo | 0.214793 | 0.223029 | 0.255004 | 0.254737 | 0.144276 | 1.000000 | 0.074030 |
| ripple | 0.105382 | 0.008049 | 0.115747 | 0.216995 | 0.152624 | 0.074030 | 1.000000 |
Info
Wir sehen, dass es keine größeren Korrelationen als .5 gibt. Ripple sticht hier etwas hervor indem es am wenigsten korreliert. Sonst ist nichts großartiges zu erkennen.
Zeitreihendekomposition Ripple
Ich werde mich nun speziell auf Ripple konzentrieren und mal eine Zeitreihendekomposition durchführen, um irgendeinen möglichen Trend, Saisonalität etc. in der Zeitreihe zu finden.
dfRipple = pd.read_csv('data/ripple_preise.csv', parse_dates=['Date'])
dfRipple.head()
dfRipple = dfRipple[['Date','Close']] #Wir wollen uns nur Datum und Schlusspreise anschauen...
dfRipple.head(3)
# Setze Date als Index
dfRipple = dfRipple.set_index('Date')
dfRipple.sort_index(inplace=True)
#dfRipple = dfRipple.resample('W').sum()
#dfRipple.isnull().sum()
#Split
split_date = pd.datetime(2017,1,1)
dfRipple = dfRipple.loc[dfRipple.index > split_date]
#dfRipple.plot()
rcParams['figure.figsize'] = 15, 10
res = sm.tsa.seasonal_decompose(dfRipple,
model='additive')
resplot = res.plot()
resplot.savefig('Seasonal_Decompose.png', dpi=150)
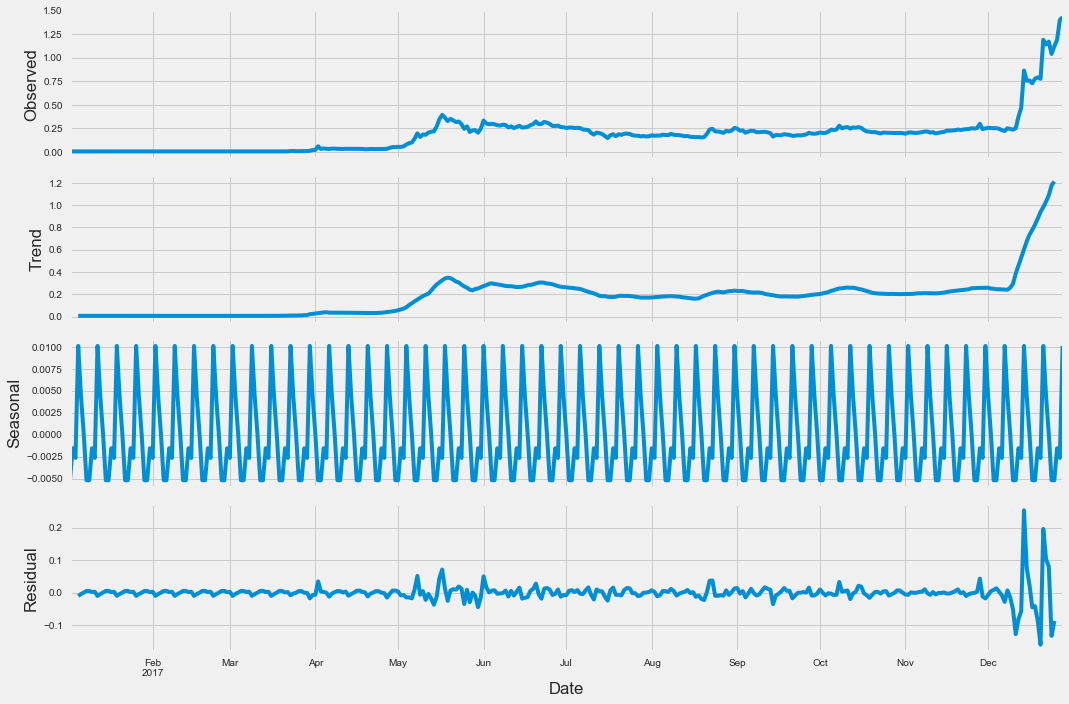
Info
Wir sehen hier eine Saisonale Zerlegung der Daten in:
- Observed sind die Originaldaten
- Saisonal ist die Wiederholung innerhalb von freq
- Trend ist der Trend
- und Residuum ist alles, was nicht durch saisonale Tendenz beschrieben wird
Es ist kein klarer Trend ersichtlich, außer, dass gegen Ende des Jahres der Kurs in die Höhe gegangen ist und bis dato noch nicht gefallen ist. Das gefällt mir!
Als Data Scientist interessiert einen natürlich wieso der Kurs im Dezember so gestiegen ist. Der Kryptomarkt ist uneinschätzbar und spekulativ, da es erstmal ein recht junger Markt ist. Man sollte sich grundsätzlich mit der Technologie einer Währung beschäftigen und sich Fragen ob man an die Technologie glaubt und ob diese Potenzial hat sich in der Zukunft beweisen zu können. Zu Beobachten ist, dass tagtäglich Nachrichten über die Kryptowelt oder speziell einer Währung im Web auftauchen. Diese Nachrichten beinhalten meistens irgendwelche Entscheidungen, Empfehlungen oder berichten darüber ob die Technologie einer Währung von einem weiteren Konzern xyz implementiert wurde. Solche Nachrichten beeinflussen den Kurs einer Währung sehr stark.
Schauen wir uns mal den Dezember genauer an…
dfRipple['2017-12-1' : '2017-12-22'].plot(figsize=(20, 10),loglog=True)
<matplotlib.axes._subplots.AxesSubplot at 0x126ea2860>
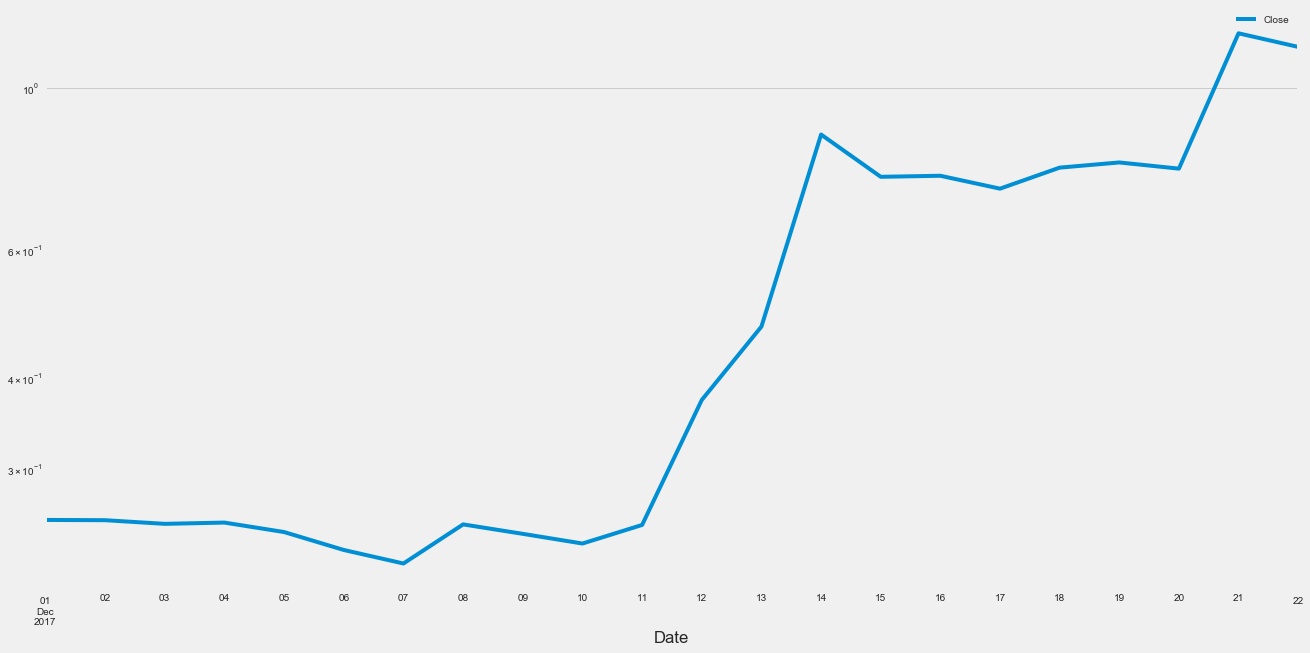
Der Anstieg ging laut Diagramm ab ca. dem 7. Dezember 2017 los. Der dominanteste Anstieg ist zwischen dem 11. und dem 14. Dezember zu beobachten. Der Kurs verdoppelte sich innerhalb der 24h vom 12. - 13. um fast 100%
Nach einer Recherche bin ich auf folgende Ereignisse gestoßen die den Anstieg des Ripple’ Kurs begründen:
-
1.12.2017 : Die Europäische Zentralbank veranstaltet die Zahlungskonferenz in Rom (30. November und 1. Dezember). Der CEO von Ripple hält eine Rede
-
6.12.2017 : Der CEO von Ripple, Brad Garlinghouse, hat an einer Podiumsdiskussion auf der Kryptoveranstaltung des MIT in San Francisco teilgenommen
-
7.12.2017: Am 07.12.2017 hat Ripple verkündet, dass die Anfangs versprochenen 55 Milliarden Ripple auf einem Treuhandkonto abgesichert werden, damit zu jedem Zeitpunkt sichergestellt ist, dass das Netzwerk im Ernstfall auch weiterhin funktioniert. Genau dieses Versprechen wurde jetzt eingelöst.
-
14.12.2017: “Banken in Japan und Südkorea beginnen Tests am Freitag der Blockchain-Technologie von US-Entwickler Ripple”
- Dadurch sollen schnellere Transaktionen realisiert werden und bis zu 30% der Kosten eingespart werden. Dabei sind 61 Banken Teil dieses Experiments. Wenn alles erfolgreich verläuft, könnten die ersten Transaktionen nächstes Jahr im Frühjahr 2018 über die Bühne gehen. Die Testphase läuft vorerst bis zum 31.01.2018.
Außerdem hat Ripple eine sehr interessante Grafik veröffentlicht, die zeigt, dass Ripple die wohl mit Abstand schnellste Kryptowähurng derzeit ist.
- Siehe:
- https://coin-hero.de/wp-content/uploads/2017/12/Ripple.png
Quellen u.a.:
- https://coin-hero.de/ripple-to-the-moon-100-kursanstieg-innerhalb-von-24h/
- https://www.ripplecoinnews.com/
- https://diepresse.com/home/wirtschaft/boerse/5337825/Die-Stunde-der-Altcoins_Litecoin-und-Ripple-schiessen-nach-oben
Ich habe mich entschieden
Ich bin von der Ripple Technologie überzeugt und werde in Ripple investieren:
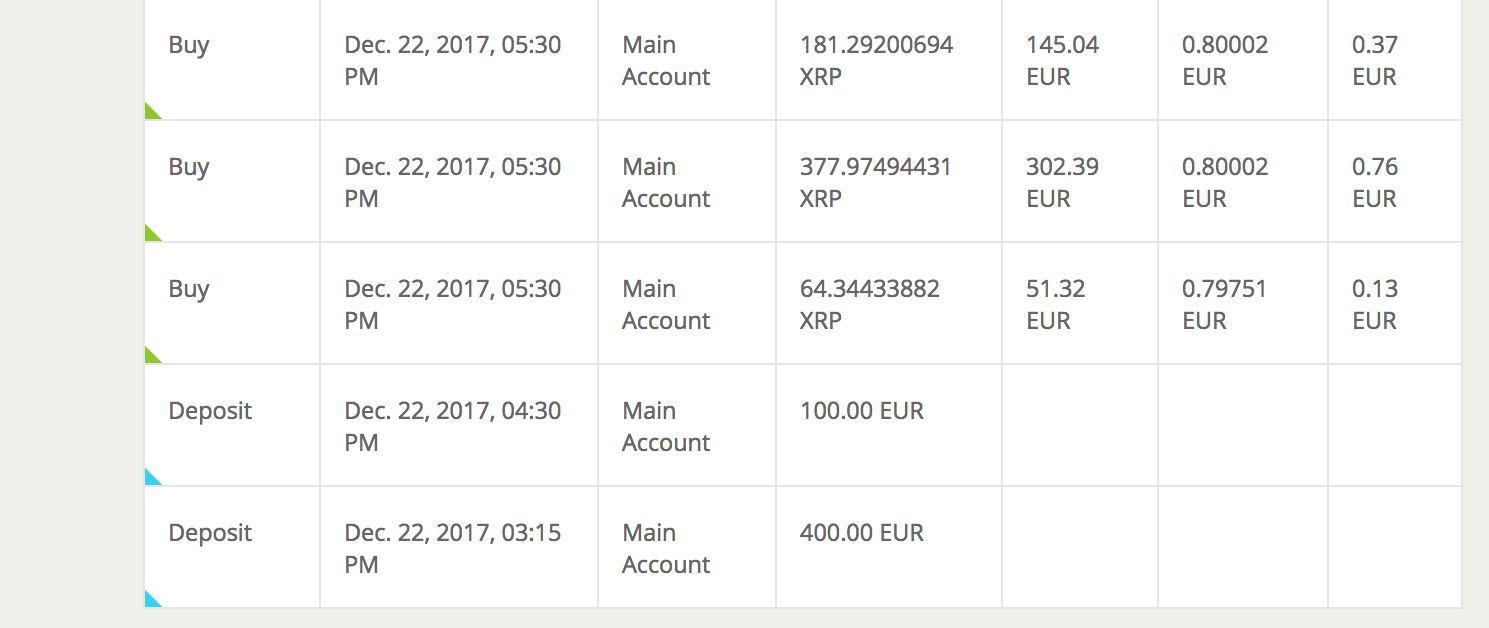
Am 22. Dezember wurden um 13:15 und 16:30 jeweils 400€ und 100€ meinem Konto gutgeschrieben.
Am selben Tag habe ich einen Kaufauftrag abgeschickt. Ich bin nun im Besitz von 623,611 XRP (Ripple). Bezahlt habe ich ~0,80€ pro Coin. Bitstamp berechnet übrigens eine Gebühr von 0.25% was bei meinem Kaufauftrag 1,25€ entspricht.
Nun heißt es abwarten!
Wo wird das meiste Kapital bewegt?
Da wir nun einfach nur warten müssen, vertreiben wir uns die Zeit mit der Beantwortung der Fragestellung wo eigentlich am meisten Kapital bewegt wird.
Um herauszufinden wo überhaupt das meiste Kapital bewegt wird, brauche ich spezifische Daten einer Exchange (oder auch genannt Börse). Dazu habe ich das erste Skript von oben womit ich mir die historischen Währungsdaten heruntergeladen habe, modifiziert:
import re
import sys
import csv
import time
import random
import requests
from datetime import date
from bs4 import BeautifulSoup
import pandas as pd
end_date = str(date.today()).replace("-","")
base_url = "https://coinmarketcap.com/exchanges/{0}/"
currency_name_list = ["bitfinex", "kraken","binance","bitstamp","Upbit","OKEx","Bithumb","Huobi","GDAX","Bittrex","HitBTC"]
def get_data(currency_name):
print("Währung : ", currency_name)
url = base_url.format(currency_name)
html_response = requests.get(url).text.encode('utf-8')
soup = BeautifulSoup(html_response, 'html.parser')
table = soup.find_all('table')[0]
elements = table.find_all("tr")
with open("data/{0}.csv".format(currency_name.replace("-","_")),"w") as ofile:
writer = csv.writer(ofile)
for element in elements:
writer.writerow( element.get_text().strip().split("\n") )
time.sleep(1)
#transformiere Daten
print(ofile.name)
DF = pd.read_csv(ofile.name,error_bad_lines=False)
DF = DF.reset_index()
DF = DF.dropna(axis=1, how='any')
DF.columns = ["#","Currency","Pair","Volume (24h)","Price","Volume (%)","Updated"]
DF = DF.drop(['#'], axis=1)
DF.to_csv(ofile.name,index=False)
if __name__ == "__main__":
for currency_name in currency_name_list:
get_data(currency_name)
pass
print("Fertig")
Währung : bitfinex
data/bitfinex.csv
Währung : kraken
data/kraken.csv
Währung : binance
data/binance.csv
Währung : bitstamp
data/bitstamp.csv
Währung : Upbit
data/Upbit.csv
Währung : OKEx
b'Skipping line 14: expected 15 fields, saw 16\nSkipping line 109: expected 15 fields, saw 17\n'
data/OKEx.csv
Währung : Bithumb
b'Skipping line 42: expected 15 fields, saw 17\nSkipping line 45: expected 15 fields, saw 17\n'
data/Bithumb.csv
Währung : Huobi
data/Huobi.csv
Währung : GDAX
data/GDAX.csv
Währung : Bittrex
data/Bittrex.csv
Währung : HitBTC
data/HitBTC.csv
Fertig
b'Skipping line 30: expected 15 fields, saw 16\nSkipping line 37: expected 15 fields, saw 16\nSkipping line 58: expected 15 fields, saw 16\nSkipping line 78: expected 15 fields, saw 16\nSkipping line 99: expected 15 fields, saw 16\nSkipping line 117: expected 15 fields, saw 16\nSkipping line 127: expected 15 fields, saw 16\nSkipping line 132: expected 15 fields, saw 16\nSkipping line 133: expected 15 fields, saw 16\nSkipping line 141: expected 15 fields, saw 16\nSkipping line 148: expected 15 fields, saw 16\nSkipping line 165: expected 15 fields, saw 16\nSkipping line 206: expected 15 fields, saw 16\nSkipping line 234: expected 15 fields, saw 16\nSkipping line 265: expected 15 fields, saw 16\nSkipping line 270: expected 15 fields, saw 16\nSkipping line 281: expected 15 fields, saw 16\nSkipping line 305: expected 15 fields, saw 16\nSkipping line 308: expected 15 fields, saw 16\nSkipping line 437: expected 15 fields, saw 16\n'
Betrachten wir doch mal exemplarisch die Daten einer Exchange…
bitfinex = pd.read_csv("data/bitfinex.csv")
bitfinex.head(10)
| Currency | Pair | Volume (24h) | Price | Volume (%) | Updated | |
|---|---|---|---|---|---|---|
| 0 | Bitcoin | BTC/USD | $461,857,000 | $10182.00 | 40.40% | Recently |
| 1 | Ethereum | ETH/USD | $126,189,000 | $940.79 | 11.04% | Recently |
| 2 | Litecoin | LTC/USD | $113,969,000 | $230.30 | 9.97% | Recently |
| 3 | Bitcoin Cash | BCH/USD | $65,444,500 | $1492.60 | 5.73% | Recently |
| 4 | Ripple | XRP/USD | $55,066,400 | $1.11 | 4.82% | Recently |
| 5 | EOS | EOS/USD | $27,329,500 | $9.83 | 2.39% | Recently |
| 6 | Tether | USDT/USD | $26,400,200 | $1.00 | 2.31% | Recently |
| 7 | Ethereum Classic | ETC/USD | $23,948,800 | $34.60 | 2.10% | Recently |
| 8 | Ethereum | ETH/BTC | $19,619,200 | $941.22 | 1.72% | Recently |
| 9 | OmiseGO | OMG/USD | $19,482,700 | $17.97 | 1.70% | Recently |
Was sehen wir?
Wir sehen hier folgende Daten des Exchanges Bitfinex:
- Currency: Die Währung um die sich die Datenzeile handelt.
- Pair: Das Verkaufspaar. Beispielweise beschreibt die erste Zeile den Kauf eines Bitcoins(BTC) per US$(USD)
- Volume (24h): Das Volumen einer Währung das in den letzten 24 Stunden auf der Exchange gehandelt wurde.
- Price: Der aktuelle Preis dieser Währung auf der Exchange. (Dieser ergibt sich übrigends durch den aktuell günstigsten angebotenen Verkaufsauftrag)
- Volume (%):: Wieviel Prozent macht diese Währung auf der Exchange aus?
- Updadet: Erklärt sich von selbst. Ist für unsere Analyse nicht weiter wichtig.
Ich habe mir elf Exchanges rausgesucht:
- Bitfinex
- Kraken
- Binance
- Bitstamp
- Upbit
- OKEx
- Bithumb
- Huobi
- GDAX
- Bittrex
- HitBTC
Zu diesen elf Exchanges habe ich mir die geographischen Koordinaten rausgesucht und manuell in eine excel Datei eingespeichert:
exchangescoord = pd.read_csv("data/exchangescoordscsv.csv",float_precision='round_trip')
exchangescoord = exchangescoord.set_index('Exchange')
exchangescoord['Longitude'] = exchangescoord['Longitude'].astype('float64')
#exchangescoord['lat_long'] = exchangescoord[['Latitude', 'Longitude']].apply(tuple, axis=1)
exchangescoord
| Region | Country | City | Latitude | Longitude | |
|---|---|---|---|---|---|
| Exchange | |||||
| Bitfinex | AS | Taiwan | Taipei | 25.105497 | 121.597366 |
| Binance | AS | Japan | Tokio | 35.661777 | 139.704051 |
| Bitstamp | EU | UK | London | 51.515675 | -0.108848 |
| Upbit | AS | South Korea | N.N | 35.907757 | 127.766922 |
| OKEx | AS | China | Hong Kong | 22.396428 | 114.109497 |
| Bithumb | AS | South Korea | Seoul | 37.498383 | 127.034131 |
| Huobi | AS | China | Peking | 39.904200 | 116.407396 |
| GDAX | US | US | New York | 40.730610 | -73.935242 |
| Bittrex | US | US | Las Vegas | 36.169941 | -115.139830 |
| HitBTC | US | US | Chicago | 41.878114 | -87.629798 |
| Kraken | US | US | San Francisco | 37.790053 | -122.400875 |
Nun haben wir eine Menge an Daten von Exchanges und die dazugehörigen geographischen Daten der Exchanges. Wir werden uns auf das Gesamtvolumen einer Exchange konzentrieren, d.h. der aufsummierte Wert der einzelnen Volumenspreise einer Währung der letzten 24 Stunden.
exchanges = {}
exchanges['bitfinex'] = pd.read_csv("data/bitfinex.csv")
exchanges['kraken'] = pd.read_csv("data/kraken.csv")
exchanges['binance'] = pd.read_csv("data/binance.csv")
exchanges['bitstamp'] = pd.read_csv("data/bitstamp.csv")
exchanges['upbit'] = pd.read_csv("data/upbit.csv")
exchanges['okex'] = pd.read_csv("data/okex.csv")
exchanges['bithumb'] = pd.read_csv("data/bithumb.csv")
exchanges['huobi'] = pd.read_csv("data/huobi.csv")
exchanges['gdax'] = pd.read_csv("data/gdax.csv")
exchanges['bittrex'] = pd.read_csv("data/bittrex.csv")
exchanges['hitbtc'] = pd.read_csv("data/hitbtc.csv")
data={'Exchange': ['Bitfinex', 'Kraken', 'Binance', 'Bitstamp', 'Upbit','OKEx','Bithumb','Huobi','GDAX','Bittrex','HitBTC']}
result = pd.DataFrame(data= data)
values = list()
for exchange in exchanges:
for column in exchanges[exchange].columns:
if column not in ['Currency', 'Volume (24h)']:
exchanges[exchange] = exchanges[exchange].drop(column, 1)
# dollar zeichen raus, kommatas raus und dtype von string zu float
exchanges[exchange]['Volume (24h)'] = exchanges[exchange]['Volume (24h)'].str.replace('$', '')
exchanges[exchange]['Volume (24h)'] = exchanges[exchange]['Volume (24h)'].str.replace(',', '')
exchanges[exchange]['Volume (24h)'] = exchanges[exchange]['Volume (24h)'].astype('float64')
values.append(exchanges[exchange]['Volume (24h)'].sum())
result['SumVolume'] = values
result = result.set_index('Exchange')
new_results = pd.concat([result, exchangescoord], axis=1)
new_results
| SumVolume | Region | Country | City | Latitude | Longitude | |
|---|---|---|---|---|---|---|
| Binance | 2.096304e+09 | AS | Japan | Tokio | 35.661777 | 139.704051 |
| Bitfinex | 1.143097e+09 | AS | Taiwan | Taipei | 25.105497 | 121.597366 |
| Bithumb | 7.329690e+08 | AS | South Korea | Seoul | 37.498383 | 127.034131 |
| Bitstamp | 2.527412e+08 | EU | UK | London | 51.515675 | -0.108848 |
| Bittrex | 3.686544e+08 | US | US | Las Vegas | 36.169941 | -115.139830 |
| GDAX | 5.480203e+08 | US | US | New York | 40.730610 | -73.935242 |
| HitBTC | 2.750893e+08 | US | US | Chicago | 41.878114 | -87.629798 |
| Huobi | 9.934975e+08 | AS | China | Peking | 39.904200 | 116.407396 |
| Kraken | 3.415304e+08 | US | US | San Francisco | 37.790053 | -122.400875 |
| OKEx | 1.828333e+09 | AS | China | Hong Kong | 22.396428 | 114.109497 |
| Upbit | 1.178377e+09 | AS | South Korea | N.N | 35.907757 | 127.766922 |
Wir haben nun ein fertiges Dataframe mit den elf gelisteten Exchanges und die dazugehörigen geogrpahischen Daten. Schauen wir uns das mal erstmal auf einer globalen Weltkarte an:
#World
# Set up plot
from mpl_toolkits.basemap import Basemap
m1 = Basemap(projection='merc',
llcrnrlat=-60,
urcrnrlat=65,
llcrnrlon=-180,
urcrnrlon=180,
lat_ts=0,
resolution='c')
m1.fillcontinents(color='#191919',lake_color='#000000') # dark grey land, black lakes
m1.drawmapboundary(fill_color='#000000') # black background
m1.drawcountries(linewidth=0.1, color="w") # thin white line for country borders
m1.drawstates(linewidth=0.1, color="w")
# Plot the data
mxy = m1(new_results["Longitude"].tolist(), new_results["Latitude"].tolist())
m1.scatter(mxy[0], mxy[1], s=300,c=np.divide(new_results["SumVolume"],100000000), lw=0, alpha=1, zorder=5,cmap='Reds')
#colorbar
plt.colorbar(label=r'24H Trading-Volumen in K-Millionen$')
plt.clim(1, 21)
plt.title("Kryptowährung Kapitalbewegung - Globale Ansicht")
plt.annotate("Globales Trading Volumen 24 Std \n "+ '${:,.2f}'.format(new_results['SumVolume'].sum()), m1(-170.704051,-40.661777),color='white')
<matplotlib.text.Annotation at 0x12232ebe0>
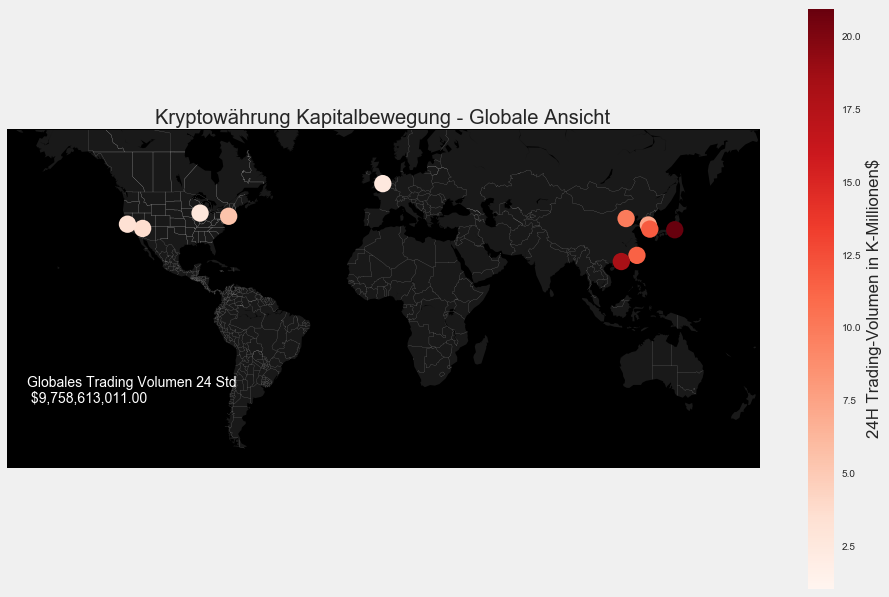
Interessant! Asien ist hier besonders Auffälig. Auf den asiatischen Exchanges wird auf dem ersten Blick weit aus mehr getradet als auf den Amerikanischen und Europäischen. Mich interessieren die Details!
#asien
# Set up plot
from mpl_toolkits.basemap import Basemap
#fig, ax = plt.subplots(figsize=(15,15))
m1 = Basemap(projection='merc',
llcrnrlat=8.3,
urcrnrlat=53.9,
llcrnrlon=94.0,
urcrnrlon=147.6,
lat_ts=0,
resolution='c')
m1.fillcontinents(color='#191919',lake_color='#000000') # dark grey land, black lakes
m1.drawmapboundary(fill_color='#000000') # black background
m1.drawcountries(linewidth=0.1, color="w") # thin white line for country borders
m1.drawstates(linewidth=0.1, color="w")
# Plot the data
mxy = m1(new_results["Longitude"].tolist(), new_results["Latitude"].tolist())
m1.scatter(mxy[0], mxy[1], s=300,c=np.divide(new_results["SumVolume"],100000000), lw=0, alpha=1, zorder=5,cmap='Reds')
plt.annotate(" Binance \n" +" " + new_results.ix['Binance'].City, m1(139.704051,35.661777),color='red')
plt.annotate(" Bitfinex \n" +" " + new_results.ix['Bitfinex'].City, m1(121.597366,25.105497),color='red')
plt.annotate(" Bithumb - " + new_results.ix['Bithumb'].City, m1(127.034131,37.498383),color='red')
plt.annotate(" Huobi \n" +" " + new_results.ix['Huobi'].City, m1(116.407396,39.904200),color='red')
plt.annotate(" OKEx \n" +" " + new_results.ix['OKEx'].City, m1(114.109497,22.396428),color='red')
plt.annotate(" Upbit - " + new_results.ix['Upbit'].City, m1(127.766922,35.907757),color='red')
#
#colorbar
plt.colorbar(label=r'24H Trading-Volumen in K-Millionen$')
plt.clim(1, 21)
plt.title("Kryptowährung Kapitalbewegung - Asien")
AS = new_results.loc[new_results['Region'] == 'AS']
print("Trading Volumen der letzten 24 Stunden, der einzelnen Exchanges aus Asien: \n")
print(AS.SumVolume.apply('${:,.2f}'.format))
print()
print("Durschnittliches Trading Volumen der asiatischen Exchanges der letzten 24 Stunden: " '${:,.2f}'.format(AS['SumVolume'].mean()))
print()
print("Gesamt-Trading Volumen aller asiatischen Exchanges der letzten 24 Stunden: "+ '${:,.2f}'.format(AS['SumVolume'].sum()))
plt.annotate(" Trading Volumen 24 Std \n "+ '${:,.2f}'.format(AS['SumVolume'].sum()), m1(130.704051,15.661777),color='white')
Trading Volumen der letzten 24 Stunden, der einzelnen Exchanges aus Asien:
Binance $2,096,304,321.00
Bitfinex $1,143,096,843.00
Bithumb $732,969,030.00
Huobi $993,497,546.00
OKEx $1,828,332,530.00
Upbit $1,178,377,133.00
Name: SumVolume, dtype: object
Durschnittliches Trading Volumen der asiatischen Exchanges der letzten 24 Stunden: $1,328,762,900.50
Gesamt-Trading Volumen aller asiatischen Exchanges der letzten 24 Stunden: $7,972,577,403.00
<matplotlib.text.Annotation at 0x12b217940>
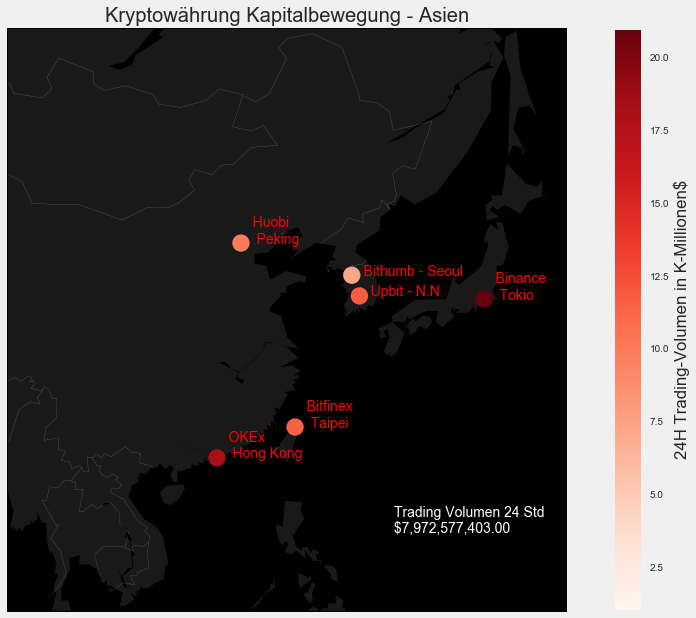
Erstaunlich! In den letzten 24 Stunden wurde verdammt viel Geld bewegt. Details finden sich über der geographischen Ansicht. Was wohl die eine Exchange aus UK umsetzt?
#eu
#1 = llcrnrlon
#2 = llcrnrlat
#3 = urcrnrlon
#4 = urcrnrlat
# Set up plot
from mpl_toolkits.basemap import Basemap
#fig, ax = plt.subplots(figsize=(15,15))
m1 = Basemap(projection='merc',
llcrnrlat=48.7,
urcrnrlat=57.85,
llcrnrlon=-8.41,
urcrnrlon=7.3,
lat_ts=0,
resolution='c')
m1.fillcontinents(color='#191919',lake_color='#000000') # dark grey land, black lakes
m1.drawmapboundary(fill_color='#000000') # black background
m1.drawcountries(linewidth=0.1, color="w") # thin white line for country borders
m1.drawstates(linewidth=0.1, color="w")
# Plot the data
mxy = m1(new_results["Longitude"].tolist(), new_results["Latitude"].tolist())
m1.scatter(mxy[0], mxy[1], s=300,c=np.divide(new_results["SumVolume"],100000000), lw=0, alpha=1, zorder=5,cmap='Reds')
plt.annotate(" Bitstamp \n" +" " + new_results.ix['Bitstamp'].City, m1(-0.108848,51.515675),color='red')
#colorbar
plt.colorbar(label=r'24H Trading-Volumen in K-Millionen$')
plt.clim(1, 21)
plt.title("Kryptowährung Kapitalbewegung - EU")
EU = new_results.loc[new_results['Region'] == 'EU']
print("Trading Volumen der letzten 24 Stunden, der einzelnen Exchanges aus Europa: \n")
print(EU.SumVolume.apply('${:,.2f}'.format))
print()
print("Durschnittliches Trading Volumen der europäischen Exchanges der letzten 24 Stunden: " '${:,.2f}'.format(EU['SumVolume'].mean()))
print()
print("Gesamt-Trading Volumen der europäischen Exchanges der letzten 24 Stunden: "+ '${:,.2f}'.format(EU['SumVolume'].sum()))
plt.annotate(" Trading Volumen 24 Std \n "+ '${:,.2f}'.format(EU['SumVolume'].sum()), m1(2.108848,56.815675),color='white')
Trading Volumen der letzten 24 Stunden, der einzelnen Exchanges aus Europa:
Bitstamp $252,741,230.00
Name: SumVolume, dtype: object
Durschnittliches Trading Volumen der europäischen Exchanges der letzten 24 Stunden: $252,741,230.00
Gesamt-Trading Volumen der europäischen Exchanges der letzten 24 Stunden: $252,741,230.00
<matplotlib.text.Annotation at 0x121e599b0>
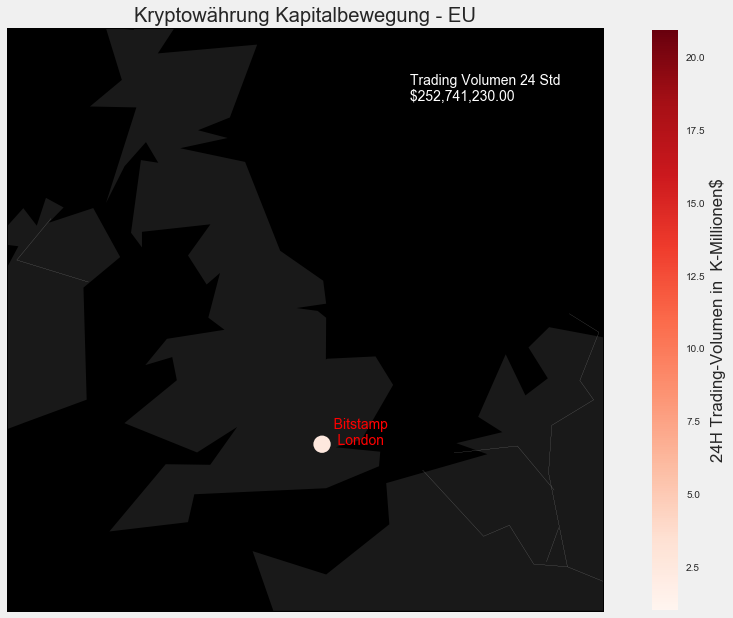
Im Vergleich zu den asiatischen Börsen ist das ein Witz. Fassen wir nochmal kurz die Werte der US Märkte zusammen.
#US
#1 = llcrnrlon
#2 = llcrnrlat
#3 = urcrnrlon
#4 = urcrnrlat
# Set up plot
from mpl_toolkits.basemap import Basemap
#fig, ax = plt.subplots(figsize=(15,15))
m1 = Basemap(projection='merc',
llcrnrlat=19.5,
urcrnrlat=60.2,
llcrnrlon=-133.9,
urcrnrlon=-62.3,
lat_ts=0,
resolution='c')
m1.fillcontinents(color='#191919',lake_color='#000000') # dark grey land, black lakes
m1.drawmapboundary(fill_color='#000000') # black background
m1.drawcountries(linewidth=0.1, color="w") # thin white line for country borders
m1.drawstates(linewidth=0.1, color="w")
# Plot the data
mxy = m1(new_results["Longitude"].tolist(), new_results["Latitude"].tolist())
m1.scatter(mxy[0], mxy[1], s=300,c=np.divide(new_results["SumVolume"],100000000), lw=0, alpha=1, zorder=5,cmap='Reds')
plt.annotate(" Bittrex - " + new_results.ix['Bittrex'].City, m1(-115.139830,36.169941),color='red')
plt.annotate(" GDAX \n" +" " + new_results.ix['GDAX'].City, m1(-73.935242,40.730610),color='red')
plt.annotate(" HitBTC - " + new_results.ix['HitBTC'].City, m1(-87.629798,41.878114),color='red')
plt.annotate(" Kraken - " + new_results.ix['Kraken'].City, m1(-122.400875,37.790053),color='red')
#colorbar
plt.colorbar(label=r'24H Trading-Volumen in K-Millionen$')
plt.clim(1, 21)
plt.title("Kryptowährung Kapitalbewegung - US")
US = new_results.loc[new_results['Region'] == 'US']
print("Trading Volumen der letzten 24 Stunden, der einzelnen Exchanges aus Amerika: \n")
print(US.SumVolume.apply('${:,.2f}'.format))
print()
print("Durschnittliches Trading Volumen der amerikanischen Exchanges der letzten 24 Stunden: " '${:,.2f}'.format(US['SumVolume'].mean()))
print()
print("Gesamt-Trading Volumen der amerikanischen Exchanges der letzten 24 Stunden: "+ '${:,.2f}'.format(US['SumVolume'].sum()))
plt.annotate(" Trading Volumen 24 Std \n "+ '${:,.2f}'.format(US['SumVolume'].sum()), m1(-78.935242,25.730610),color='white')
Trading Volumen der letzten 24 Stunden, der einzelnen Exchanges aus Amerika:
Bittrex $368,654,368.00
GDAX $548,020,280.00
HitBTC $275,089,306.00
Kraken $341,530,424.00
Name: SumVolume, dtype: object
Durschnittliches Trading Volumen der amerikanischen Exchanges der letzten 24 Stunden: $383,323,594.50
Gesamt-Trading Volumen der amerikanischen Exchanges der letzten 24 Stunden: $1,533,294,378.00
<matplotlib.text.Annotation at 0x12214c3c8>
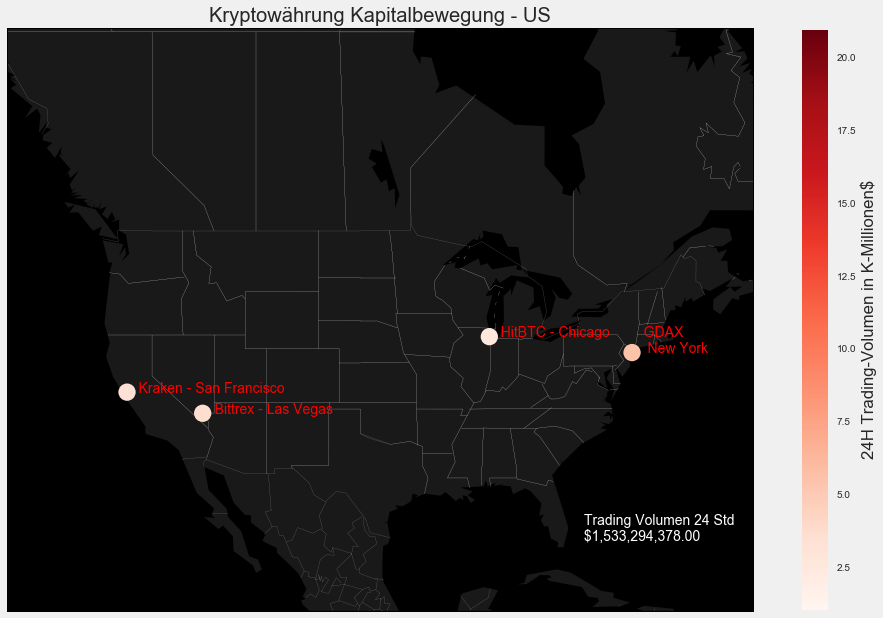
Wir sehen: Die Asiaten sind sehr gut dabei, gefolgt von den Amerikanern und letzendlich den Europäern. Man beachte, dass ich hier nur eine Auswahl der größten exchanges getroffen habe. Es gibt noch einige andere kleinere Exchanges, welche aber von den elf gelisteten Exchanges nur einen sehr kleinen Bruchteil an Kapital bewegen.
Was macht unser Invest?
Wir haben mittlerweile den 12.Februar 2018. Es sind nun 52 Tage seit unserem inital Invest um. In dieser Zeit lief der Kurs hoch und runter. Wir visualieren uns das am besten mal mit Hilfe der plotly-library. Die plotly-library gibt uns die Möglichkeit interaktive Plots zu erzeugen. Wie cool!
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
from plotly.graph_objs import Scatter, Figure, Layout
import plotly.graph_objs as go
init_notebook_mode(connected=True)
ripple = pd.read_csv("datas/ripple_preise.csv", parse_dates=['Date'])
ripple['Date'] = pd.to_datetime(ripple['Date'])
ripple = ripple[ripple['Date'] >= '2017-12-22']
ripple = ripple.sort_values('Date')
ripple = ripple.reset_index()
arr = np.empty(ripple['Date'].size)
arr.fill(593.125)
plot0 = go.Scatter(
x = ripple['Date'],
y = arr,
mode = 'lines',
name = 'Investment'
)
plot1 = go.Scatter(
x = ripple['Date'],
y = 593.125 * ripple['Close'].astype(float), #Wir müssen unsere 500€ (abzüglich 1,25€ Fee) start-invest als $Dollar Wert anzeigen. Dieser war am 22.Dezember 2017 bei 593,125$. Wir möchten hier ja nicht schummeln.
mode = 'lines',
name = 'Kontoguthaben'
)
plot2 = go.Scatter(
x = ripple['Date'],
y = ripple['Close'].astype(float),
mode = 'lines',
name = 'Ripple Preis'
)
plot_data = [plot0, plot1, plot2]
iplot(plot_data)
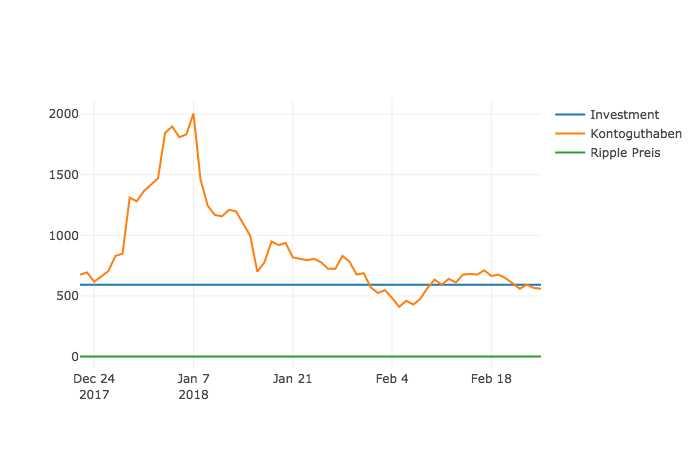
Oh Mann! Hier sieht man doch wie volatil der Markt ist. Mein Invest hatte bis dato am 7.Januar 2018 seinen maximalen Wert von 2004,7$. Bis dahin sah es sehr gut aus, doch dann kam eine Kurskorrektur. Auf diese Kurskorrektur werde ich hier jetzt nicht eingehen, aber kurz zusammengefasst: Jede Kryptowährung ist in den letzten zwei Wochen sehr stark gefallen. Bis zum 07.Januar 2018 hat der Ripple eine prozentuale Veränderung von +196.49%. Wow! Hoffentlich kommt der Kurs da schnell wieder an - Ich bin da ziemlich zuversichtlich. Kurzzeitig war ich sogar unter meinem Invest, aber wie man sieht geht der Preis wieder hoch.
Wir träumen kurz
Wir stellen uns mal kurz vor: Was wäre eigentlich gewesen wenn ich 2015 in den Bitcoin eingestiegen wäre? Genauer: Wo würde ich jetzt stehen, wenn ich seit dem 01.01.2015 jeden Tag 15€ in den Bitcoin investiert hätte:
BTC = pd.read_csv("datas/bitcoin_preise.csv", parse_dates=['Date'])
BTC['Date'] = pd.to_datetime(BTC['Date'])
BTC = BTC[BTC['Date'] >= '2015-01-01']
BTC = BTC.sort_values('Date')
BTC = BTC.reset_index()
plot0 = go.Scatter(
x = BTC['Date'],
y = (BTC.index+1)*15,
mode = 'lines',
name = 'Investment'
)
plot1 = go.Scatter(
x = BTC['Date'],
y = ((15.0 / BTC['Close'].astype(float)).cumsum()) * BTC['Close'].astype(float),
mode = 'lines',
name = 'Kontoguthaben'
)
plot2 = go.Scatter(
x = BTC['Date'],
y = BTC['Close'].astype(float),
mode = 'lines',
name = 'Bitcoin Preis'
)
plot_data = [plot0, plot1, plot2]
iplot(plot_data)
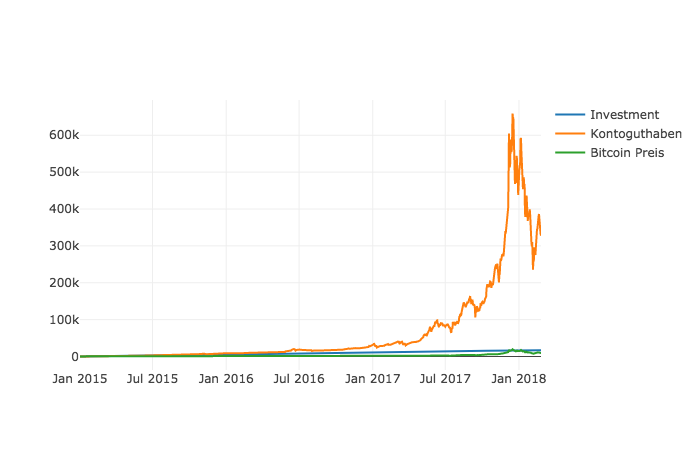
Na ob uns das überrascht? Eher nicht, der Kontoguthaben-Graph spricht Bände. Hätte ich dem Bitcoin doch 2015 mal mehr Aufmerksamkeit geschenkt.
Aber nunja: ** Hätte Hätte Blockchain Kette! **
Wir möchten den Ripple-Wert prognostizieren!
Wir werden ein RNN (Rekurrentes neuronales Netz) zum vorhersagen des Ripple Kurses einsetzen. Auf die Theorie des RNN werde ich hier nicht weiter eingehen. Im großen WWW gibt es zahlreiche Erklärungen auf die ich gerne weiter verweise.
Das aufsetzen eines Prognosemodells geschieht in drei Schritten:
- Datenaufbereitung
- Trainieren des Modells
- Prognosenabfrage
Wir werden hier den Tagesabschluss-Preis betrachten. Als erstes werden die Daten eingelesen
# Importiere die Daten...
df = pd.read_csv("datas/ripple_preise.csv", parse_dates=['Date'])
df['date'] = df['Date']
group = df.groupby('date')
rp = group['Close'].mean()
rp.head()
date
2013-08-04 0.005882
2013-08-05 0.005613
2013-08-06 0.004680
2013-08-07 0.004417
2013-08-08 0.004254
Name: Close, dtype: float64
Wir splitten unsere Daten in einen Trainings- und Testdatensatz auf. Ich möchte den Ripple-Preis für ca. einen Monat vorhersagen, daher nehme ich die Daten der letzten 35 Tage als Testmenge
# split data
pred = 35
df_train= rp[:len(rp)-pred]
df_test= rp[len(rp)-pred:]
Bevor wir die Daten in das Neuronale Netz schicken, skalieren wir die Daten in einen neuen Wertebereich. Dies tun wir, weil unser Prognosemodell die sigmoide Aktivierungsfunktion nutzt und somit nur Werte zwischen 0 und 1 verarbeiten kann. Zusätzlich definieren wir unsere Eingangsdaten und Ausgangsdaten.
# Datenvorverarbeitung
training_set = df_train.values
training_set = np.reshape(training_set, (len(training_set), 1))
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler()
training_set = sc.fit_transform(training_set)
X_train = training_set[0:len(training_set)-1]
y_train = training_set[1:len(training_set)]
X_train = np.reshape(X_train, (len(X_train), 1, 1))
Nun bauen wir das Prognosemodell. Hierzu nutzen wir das Keras Framework. Dies ist eine recht populäres Deep Learning Bibliothek die auf Google’ Tensorflow oder Theano aufbaut und die Abstraktionsebene nochmal etwas anhebt. Unser Prognosemodell besteht aus einem Eingabelayer, einem Verarbeitungslayer (ein LSTM) und einem Ausgabelayer.
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
# Initialisere das RNN
regressor = Sequential()
# Füge den input und den LSTM Layer hinzu
regressor.add(LSTM(units = 4, activation = 'sigmoid', input_shape = (None, 1)))
# Füge output Layer hinzu
regressor.add(Dense(units = 1))
# Waehle den adam optimierer aus und den MSE als Fehlerfunktion
regressor.compile(optimizer = 'adam', loss = 'mean_squared_error')
# trainiere das RNN mit unseren Trainingsdaten, 100 Epochen lang
regressor.fit(X_train, y_train, batch_size = 5, epochs = 100)
Using TensorFlow backend.
Epoch 1/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0304
Epoch 2/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0064
Epoch 3/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0061
Epoch 4/100
1621/1621 [==============================] - 2s 2ms/step - loss: 0.0058
Epoch 5/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0055
Epoch 6/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0052
Epoch 7/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0049
Epoch 8/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0046
Epoch 9/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0043
Epoch 10/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0041
Epoch 11/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0038
Epoch 12/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0035
Epoch 13/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0032
Epoch 14/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0028
Epoch 15/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0025
Epoch 16/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0022
Epoch 17/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0019
Epoch 18/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0016
Epoch 19/100
1621/1621 [==============================] - 3s 2ms/step - loss: 0.0013
Epoch 20/100
1621/1621 [==============================] - 2s 1ms/step - loss: 0.0011
Epoch 21/100
1621/1621 [==============================] - 2s 1ms/step - loss: 8.4993e-04
Epoch 22/100
1621/1621 [==============================] - 3s 2ms/step - loss: 6.6817e-04
Epoch 23/100
1621/1621 [==============================] - 3s 2ms/step - loss: 5.1442e-04
Epoch 24/100
1621/1621 [==============================] - 3s 2ms/step - loss: 3.8742e-04
Epoch 25/100
1621/1621 [==============================] - 2s 2ms/step - loss: 2.9531e-04
Epoch 26/100
1621/1621 [==============================] - 2s 1ms/step - loss: 2.4015e-04
Epoch 27/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.9840e-04
Epoch 28/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.7844e-04
Epoch 29/100
1621/1621 [==============================] - 4s 2ms/step - loss: 1.6600e-04
Epoch 30/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.6190e-04
Epoch 31/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.6025e-04
Epoch 32/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5923e-04
Epoch 33/100
1621/1621 [==============================] - 2s 2ms/step - loss: 1.5724e-04
Epoch 34/100
1621/1621 [==============================] - 2s 2ms/step - loss: 1.6021e-04
Epoch 35/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5532e-04
Epoch 36/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5849e-04
Epoch 37/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.6122e-04
Epoch 38/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5507e-04
Epoch 39/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5926e-04
Epoch 40/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5833e-04
Epoch 41/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5774e-04
Epoch 42/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5922e-04
Epoch 43/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.6044e-04
Epoch 44/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.6018e-04
Epoch 45/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5691e-04
Epoch 46/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5622e-04
Epoch 47/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5436e-04
Epoch 48/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4942e-04
Epoch 49/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5406e-04
Epoch 50/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5382e-04
Epoch 51/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5157e-04
Epoch 52/100
1621/1621 [==============================] - 2s 998us/step - loss: 1.5486e-04
Epoch 53/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5288e-04
Epoch 54/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5334e-04
Epoch 55/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5376e-04
Epoch 56/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5125e-04
Epoch 57/100
1621/1621 [==============================] - 2s 2ms/step - loss: 1.5207e-04
Epoch 58/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.4875e-04
Epoch 59/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5230e-04
Epoch 60/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5386e-04
Epoch 61/100
1621/1621 [==============================] - 2s 2ms/step - loss: 1.4744e-04
Epoch 62/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.5180e-04
Epoch 63/100
1621/1621 [==============================] - 5s 3ms/step - loss: 1.5186e-04
Epoch 64/100
1621/1621 [==============================] - 4s 3ms/step - loss: 1.4900e-04
Epoch 65/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4773e-04
Epoch 66/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5113e-04
Epoch 67/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5272e-04
Epoch 68/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5255e-04
Epoch 69/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5068e-04
Epoch 70/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4733e-04
Epoch 71/100
1621/1621 [==============================] - 2s 995us/step - loss: 1.4990e-04
Epoch 72/100
1621/1621 [==============================] - 2s 947us/step - loss: 1.4681e-04
Epoch 73/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4825e-04
Epoch 74/100
1621/1621 [==============================] - 2s 2ms/step - loss: 1.4761e-04
Epoch 75/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4949e-04
Epoch 76/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4969e-04
Epoch 77/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4801e-04
Epoch 78/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4803e-04
Epoch 79/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4893e-04
Epoch 80/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.5074e-04
Epoch 81/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4960e-04
Epoch 82/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4828e-04
Epoch 83/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4771e-04
Epoch 84/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4593e-04
Epoch 85/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.4618e-04
Epoch 86/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4592e-04
Epoch 87/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.4868e-04
Epoch 88/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.4922e-04
Epoch 89/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4910e-04
Epoch 90/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4775e-04
Epoch 91/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4616e-04
Epoch 92/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4434e-04
Epoch 93/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.4394e-04
Epoch 94/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4993e-04
Epoch 95/100
1621/1621 [==============================] - 3s 2ms/step - loss: 1.4502e-04
Epoch 96/100
1621/1621 [==============================] - 2s 2ms/step - loss: 1.4525e-04
Epoch 97/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4694e-04
Epoch 98/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4695e-04
Epoch 99/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4703e-04
Epoch 100/100
1621/1621 [==============================] - 2s 1ms/step - loss: 1.4489e-04
<keras.callbacks.History at 0x125af8fd0>
Das Modell ist nun trainiert. Kommen wir zum 3. Schritt –> Der Prognose. Es gibt es zu Beachten, dass hier der Preis des nächsten Tages nur anhand dem heutigen Preis vorhergesagt wird.
In der Praxis haben wir natürlich noch viele weitere Einflussfaktoren die unseren Wert beeinflussen. Auf diese werden wir hier aber nicht weiter gehen. Es sollte also klar sein, dass wenn wir einen längeren Zeitraum prognostizieren wollen, wir auch ziemlich unsaubere Prognosen erhalten.
# prognostiziere und transformiere daten zurueck...
test_set = df_test.values
inputs = np.reshape(test_set, (len(test_set), 1))
inputs = sc.transform(inputs)
inputs = np.reshape(inputs, (len(inputs), 1, 1))
pred_ripple = regressor.predict(inputs)
pred_ripple = sc.inverse_transform(pred_ripple)
Wir plotten nun den vorhergesagten und den realen Preis. Da es im letzten Monat eher weniger Schwankungen gab, kommen wir garnicht mal so schlechte Ergebnisse. Das wird sich aber ganz klar ändern wenn wir über einen Monat hinaus prognostizieren.
# Visualisiere
plt.figure(figsize=(25,15), dpi=80, facecolor='w', edgecolor='k')
ax = plt.gca()
plt.plot(test_set, color = 'red', label = 'Tatsächlicher Ripple Preis')
plt.plot(pred_ripple, color = 'blue', label = 'Vorhergesagter Ripple Preis')
plt.title('Ripple Preisvorhersage', fontsize=40)
df_test = df_test.reset_index()
x=df_test.index
labels = df_test['date']
plt.xticks(x, labels, rotation = 'vertical')
for tick in ax.xaxis.get_major_ticks():
tick.label1.set_fontsize(18)
for tick in ax.yaxis.get_major_ticks():
tick.label1.set_fontsize(18)
plt.xlabel('Zeit', fontsize=40)
plt.ylabel('Ripple Preis(USD)', fontsize=40)
plt.legend(loc=2, prop={'size': 25})
plt.show()
def rmse(predictions, targets):
return np.sqrt(((predictions - targets) ** 2).mean())
rmse_val = rmse(np.array(pred_ripple), np.array(test_set))
print("rms error ist: " + str(rmse_val))

rms error ist: 0.541578700466
Das Erstellen eines Vorhersagemodells ist nur der erste Teil eines Vorhersagesystems. Modelle müssen normalerweise objektiv gegeneinander evaluiert werden, um zu bestimmen, welches Modell verwendet werden soll. Beim maschinellen Lernen ist es daher üblich, die Vorhersagen aus dem Testsatz zu verwenden und diese mit den tatsächlichen Daten unter Verwendung von Qualitätsmaßen zu vergleichen. Solche Qualitätsmaße sind Funktionen, die angeben wie gut eine Funktionskurve an vorliegende Daten angepasst ist.
Regressionsmetrik - Root mean squared error (RMSE)
Die am häufgisten verwendete Metrik für Regressionsprobleme ist der der RSMSE, welcher definiert ist als die Quadratwurzel der durchschnittlichen quadratischen Entfernung zwischen den tatsächlichen Beobachtungswerten und der Prognose. Genauer beantwortet der RMSE die Frage: “Wie ähnlich sind im Durchschnitt die Zahlen aus Liste1 und Liste2?”. Diese zwei Listen müssen die gleiche Größe haben. Man möchte damit gewissermaßen das Rauschen zwischen zwei gegebenen Elementen und die Größe der gesammelten Daten auswaschen, um ein einheitliches Gefühl für Veränderungen im Laufe der beobachteten Zeit zu bekommen.
Wir haben einen RMSE von 0,54$. Ich würde mal sagen nicht schlecht! Wir sollten aber beachten, dass der Riplle Preis in einem kleinen Zahlenbereich hin und her schwankt, da ist ein durchschnittlicher Fehler von 50$-Cents nicht gerade wenig. Der Markt befindet sich zusätzlich in den letzten Tagen in einer Korrekturphase, wo er nicht viel hin und her springt. Eine Prognose bei 60 Tagen Rücklauf würde wohl nicht so gut verlaufen.
