Feature Selection für Machine Learning - Predictive Analytics - Teil 1

Monday. March 12, 2018 - 13 mins

Einleitung
Univariate Merkmalauswahl
Korrelationskoeffizient
Modellbasiertes Ranking

Einleitung

Der richtige Umgang mit der Merkmalsauswahl für Vorhersagemodelle ist für einen Data Scientist oder Machine Learning Spezialist ein großer Vorteil. Auf die Frage, welche Features nun genutzt werden sollen, um ein Vorhersagemodell zu erstellen gibt es erstmal keine klare Antwort. Meistens ist Domäne Wissen notwendig um solch eine Problemstellung überhaupt zu lösen. Der Prozess des Feature Selection soll uns unsere relevantesten Merkmale bzw. Features für unser Problem automatisch auswählen, denn die Auswahl richtiger Merkmale hat einen sehr großen Einfluss auf die Leistung unserer maschinellen Lernmodelle. Hier gibt es zu beachten, dass sich schlechte oder irrelevante Merkmale meistens negativ auf die Modellleistung auswirken. Um das zu vermeiden, kann man einige Verfahren zur richtigen Merkmalsauswahl benutzen. Es gilt grundsätzlich: Nicht alle Merkmale sind gleich zu behandeln. Mehr Merkmale bedeutet nicht, dass unser Lernmodell performanter sein wird. Mehr ist nicht immer besser.

Macht man sich mal gründlicher Gedanken darüber, welche Vorteile uns eigentlich eine korrekte Merkmalsauswahl bringt, fallen mir Drei Vorteile ein:

Weniger Überanpassung: Minimieren oder entfernen wir redundante Daten, hat das trainierte Modell weniger Möglichkeiten statische Vorhersagen zu treffen.
Verbesserte Präzision: je weniger schlechte Daten eingesetzt werden, desto bessere Ergebnisse liefert uns ein Prognosemodell.
Konzentration auf das wesentliche: Dies führt zu einer reduzierten Trainingszeit der Machine Learning Modelle. Hier gilt, weniger Daten implizieren, dass Algorithmen schneller trainieren.

Wer sich für mehr Theorie Wissen begeistern kann, dem empfehle ich folgenden Blogeintrag von Machine-Learning-Mastery: https://machinelearningmastery.com/an-introduction-to-feature-selection/

Diese Blogreihe soll einige Möglichkeiten darstellen, wie man verschiedene Ansätze zur richtigen Feature-Auswahl umsetzt. Dazu konzentriere ich mich hier auf Regressionsdatensätze. Das meiste von dem was euch in Zukunft erwartet ist aber auch auf Klassifikations-Modelle anwendbar.

Univariate Merkmalauswahl

Der erste Teil der Reihe wird sich mit Verfahren zur univariaten Merkmalsauswahl beschäftigen. Solche Verfahren untersuchen die Stärke der Beziehung jeder Merkmale zu der Zielvariable. Sie helfen gut dabei, diejenigen Merkmale auszuwählen, die die stärkste Beziehung zu den Zielvariablen haben. Sie helfen uns zusätzlich die Struktur und Eigenschaften der Daten besser zu verstehen. So kann man initial zwischen guten und schlechten Merkmale trennen.

Korrelationskoeffizient

Als erstes möchte ich den Korrelationskoeffizienten vorstellen. Dieser gehört zu den simpelsten und einfachsten Methoden, um die Beziehung der Merkmale zu der Zielvariable zu verstehen. Ich werde nicht auf die mathematische Definition des Korrelationskoeffizienten eingehen, aber grundsätzlich wird hier die lineare Korrelation zwischen zwei Variablen gemessen. Als Ergebnis erhält man einen Wert, welcher in [-1; 1] liegt. Nimmt eine variable zu und die andere ab und der Korrelationswert beträgt -1, sprechen wir von einer perfekten negativen Korrelation. 1 steht folglich für eine perfekte positive Korrelation.

Als Datensatz nutze ich hier einen Datensatz aus Kaggle, der als Zielvariable den Verkaufspreis einer Immobilie in Dollar aufweist. Als Features haben wir eine Reihe von nützlichen Attributen, wie Grundstückfläche, Wohnfläche, Kellerfläche, Garagenfläche, Anzahl der Zimmer….und und und. Weitere Infos findest du hier: https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data

Die Seaborn Bibliothek bietet uns eine ziemlich komfortable Möglichkeit die Korreleationen zu visualieren; als Heatmap:

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")

#correlation matrix
corrmat = train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);

png

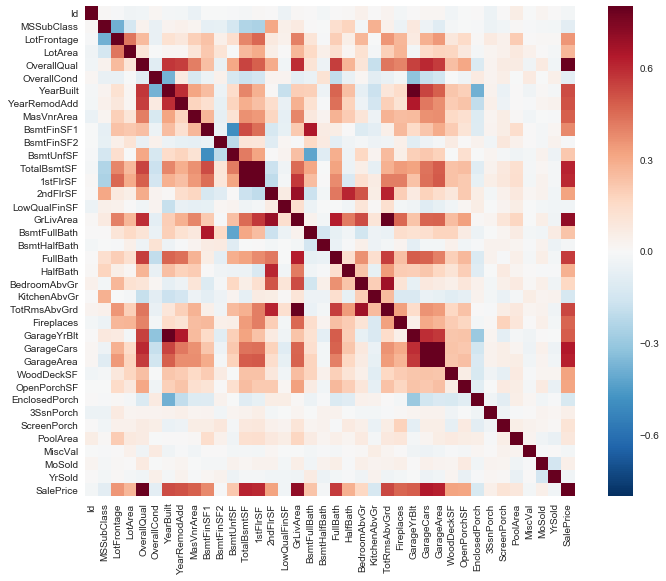
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

png

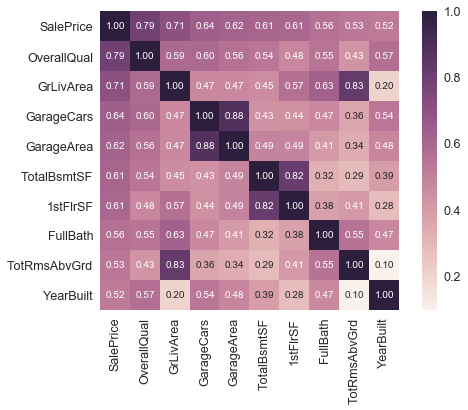
Auffällig hier sind die Variablen “TotalBsmtSF” und “1stFlrSF”, und außerdem die Beziehung der Variablen mit einem “Garage” im Namen. Wir sehen hier eine signifikante Korrelation miteinander. In der Regel bedeutet sowas, dass diese Merkmale uns quasi dieselben Informationen liefern und dadurch zumindest einer wegfallen kann. Diese Beobachtung nennt man eine Multikollinearität, was nahelegt, dass zwei oder mehrere Variablen in der Regressionsanalyse eine sehr starke Korrelation miteinander haben.

Eine weitere nützliche Beobachtung sind die Korrelationen von unserer Zielvariable SalesPrice. Die Variablen “GrLivArea”, “TotalBsmtSF” und “OverallQual” liefern hier ziemlich gute Werte. Auch viele andere Features sollten laut der oberen komprimierten Heatmap beachtet werden.

Folgende Merkmale sind wohl die am meisten korrelierten Variablen mit unserer Zielvariable und scheinen wichtig zu sein:

‘OverallQual’, ‘GrLivArea’ und ‘TotalBsmtSF’ sind stark mit ‘SalePrice’ korreliert.
“GarageArea” und “GarageCars” wie oben schon erwähnt: Eine Variable kann weg. Am besten behalten wir “GarageArea”, da diese höher mit der Zielvariable korreliert.
“TotalBsmtSF” und “1stFloor” zeigt ebenfalls eine Multikollinearität. Einer kann Weg.
“TotRmsAbvGrd” und “GrLivArea” zeigt ebenfalls eine Multikollinearität. Einer kann Weg.
“YearBuilt” ist nur leicht mit SalePrice korreliert, aber wohl trotzdem wichtig.

Modellbasiertes Ranking

Als nächstes Verfahren wird ein Modellbasiertes Ranking vorgestellt.

Es wird ein Maschinelles Lernverfahren angewendet, um ein Prognosemodell für unsere Zielvariable zu trainieren, wo jedes Merkmal einzeln betrachtet wird. Anschließend wird die Leistung des Modells gemessen.

In unserem Fall wird ein RandomForestRegressor aufgesetzt. Die tiefe der Bäume wird niedrig gehalten, um eine Überanpassung des Modells zu umgehen.

Da das trainieren eines Modells ohne Aufbereitung der Daten nicht einfach passieren soll, müssen unsere Daten erstmal aufbereitet werden. Das bedeutet:

Finden aller kategorischen Daten
Kontinuierliche und kategorische Daten trennen
Behandlung der fehlenden Daten für kontinuierliche Daten
Behandlung der fehlenden Daten für die kategorischen Daten
Zusammenführen der Daten

Mehr Dazu Siehe: https://www.kaggle.com/dfitzgerald3/randomforestregressor

from scipy.stats import skew
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import LabelEncoder

target = train[train.columns.values[-1]]

def is_outlier(points, thresh = 3.5):
    if len(points.shape) == 1:
        points = points[:,None]
    median = np.median(points, axis=0)
    diff = np.sum((points - median)**2, axis=-1)
    diff = np.sqrt(diff)
    med_abs_deviation = np.median(diff)

    modified_z_score = 0.6745 * diff / med_abs_deviation

    return modified_z_score > thresh

#Kontinuierliche Daten aufbereiten..
cats = []
for col in train.columns.values:
    if train[col].dtype == 'object':
        cats.append(col)
df_cont = train.drop(cats, axis=1)
df_cat = train[cats]

for col in df_cont.columns.values:
    if np.sum(df_cont[col].isnull()) > 50:
        df_cont = df_cont.drop(col, axis = 1)
    elif np.sum(df_cont[col].isnull()) > 0:
        median = df_cont[col].median()
        idx = np.where(df_cont[col].isnull())[0]
        df_cont[col].iloc[idx] = median

        outliers = np.where(is_outlier(df_cont[col]))
        df_cont[col].iloc[outliers] = median

        if skew(df_cont[col]) > 0.75:
            df_cont[col] = np.log(df_cont[col])
            df_cont[col] = df_cont[col].apply(lambda x: 0 if x == -np.inf else x)

        df_cont[col] = Normalizer().fit_transform(df_cont[col].reshape(1,-1))[0]


#Kategorische Daten aufbereiten...

for col in df_cat.columns.values:
    if np.sum(df_cat[col].isnull()) > 50:
        df_cat = df_cat.drop(col, axis = 1)
        continue
    elif np.sum(df_cat[col].isnull()) > 0:
        df_cat[col] = df_cat[col].fillna('MIA')

    df_cat[col] = LabelEncoder().fit_transform(df_cat[col])

    num_cols = df_cat[col].max()
    for i in range(num_cols):
        col_name = col + '_' + str(i)
        df_cat[col_name] = df_cat[col].apply(lambda x: 1 if x == i else 0)

    df_cat = df_cat.drop(col, axis = 1)


#Zusammenführen...
df_new = df_cont.join(df_cat)
df_new = df_new.drop('SalePrice', 1)
x = df_new
y = target

Nun sind die Daten aufbereitet und können endlich dem RandomForest Regressor übergeben werden:

from sklearn.ensemble import RandomForestRegressor
from sklearn.cross_validation import cross_val_score, ShuffleSplit




x = df_new
y = target
feat_labels = x.columns
x = x.values

rf = RandomForestRegressor(n_estimators=20, max_depth=4)
scores = []
for i in range(x.shape[1]):
     score = cross_val_score(rf, x[:, i:i+1], y, scoring="r2",
                              cv=ShuffleSplit(len(x), 3, .3))
     scores.append((round(np.mean(score), 3), feat_labels[i]))
print(sorted(scores, reverse=True))

/Users/Tareq/anaconda/lib/python3.6/site-packages/sklearn/cross_validation.py:44: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also note that the interface of the new CV iterators are different from that of this module. This module will be removed in 0.20.
  "This module will be removed in 0.20.", DeprecationWarning)


[(0.63300000000000001, 'OverallQual'), (0.51100000000000001, 'GrLivArea'), (0.51000000000000001, 'GarageCars'), (0.40899999999999997, 'TotalBsmtSF'), (0.40899999999999997, 'GarageArea'), (0.38, '1stFlrSF'), (0.35899999999999999, 'FullBath'), (0.31900000000000001, 'YearBuilt'), (0.28100000000000003, 'Foundation_2'), (0.26500000000000001, 'BsmtQual_0'), (0.26200000000000001, 'TotRmsAbvGrd'), (0.25700000000000001, 'YearRemodAdd'), (0.248, 'KitchenQual_0'), (0.23999999999999999, 'MSSubClass'), (0.22600000000000001, 'ExterQual_2'), (0.221, 'ExterQual_0'), (0.22, 'BsmtFinSF1'), (0.20799999999999999, 'LotArea'), (0.19700000000000001, 'Fireplaces'), (0.189, 'HeatingQC_0'), (0.17899999999999999, 'OpenPorchSF'), (0.17599999999999999, '2ndFlrSF'), (0.16300000000000001, 'BsmtFinType1_2'), (0.14299999999999999, 'Neighborhood_16'), (0.126, 'Foundation_1'), (0.107, 'MasVnrType_3'), (0.106, 'SaleType_6'), (0.099000000000000005, 'Neighborhood_15'), (0.098000000000000004, 'OverallCond'), (0.096000000000000002, 'HalfBath'), (0.094, 'KitchenQual_2'), (0.094, 'Exterior2nd_13'), (0.081000000000000003, 'WoodDeckSF'), (0.074999999999999997, 'BsmtExposure_1'), (0.073999999999999996, 'Exterior1st_12'), (0.070000000000000007, 'HouseStyle_5'), (0.060999999999999999, 'CentralAir_0'), (0.056000000000000001, 'MSZoning_3'), (0.053999999999999999, 'RoofStyle_3'), (0.053999999999999999, 'MasVnrType_1'), (0.050999999999999997, 'RoofStyle_1'), (0.050000000000000003, 'BsmtQual_2'), (0.042000000000000003, 'Electrical_0'), (0.040000000000000001, 'Neighborhood_22'), (0.039, 'BsmtFullBath'), (0.037999999999999999, 'Neighborhood_17'), (0.037999999999999999, 'BsmtUnfSF'), (0.033000000000000002, 'SaleCondition_4'), (0.033000000000000002, 'Exterior1st_8'), (0.032000000000000001, 'Neighborhood_12'), (0.029999999999999999, 'Foundation_0'), (0.029000000000000001, 'Neighborhood_7'), (0.028000000000000001, 'BsmtCond_2'), (0.025999999999999999, 'BsmtFinType2_4'), (0.025000000000000001, 'KitchenAbvGr'), (0.025000000000000001, 'Exterior2nd_8'), (0.025000000000000001, 'Exterior2nd_14'), (0.023, 'PavedDrive_0'), (0.023, 'Neighborhood_9'), (0.023, 'LotShape_0'), (0.023, 'BsmtExposure_2'), (0.021000000000000001, 'Neighborhood_3'), (0.021000000000000001, 'BsmtQual_3'), (0.02, 'LotShape_1'), (0.019, 'Exterior2nd_5'), (0.019, 'Condition1_2'), (0.017999999999999999, 'HouseStyle_0'), (0.017999999999999999, 'BldgType_0'), (0.017000000000000001, 'KitchenQual_1'), (0.017000000000000001, 'BsmtCond_0'), (0.016, 'BsmtQual_1'), (0.016, 'BedroomAbvGr'), (0.014999999999999999, 'Neighborhood_21'), (0.014999999999999999, 'Neighborhood_19'), (0.014999999999999999, 'Exterior2nd_0'), (0.014999999999999999, 'EnclosedPorch'), (0.014999999999999999, 'BsmtFinType1_4'), (0.014, 'SaleCondition_0'), (0.012999999999999999, 'Neighborhood_10'), (0.012999999999999999, 'LotConfig_1'), (0.012999999999999999, 'HeatingQC_2'), (0.012, 'Exterior1st_13'), (0.012, 'Exterior1st_0'), (0.012, 'Condition1_0'), (0.010999999999999999, 'MSZoning_0'), (0.010999999999999999, 'HeatingQC_1'), (0.01, 'Neighborhood_23'), (0.01, 'Electrical_1'), (0.0089999999999999993, 'Condition1_1'), (0.0089999999999999993, 'BsmtFinType1_5'), (0.0089999999999999993, 'BsmtFinType1_3'), (0.0089999999999999993, 'BldgType_2'), (0.0080000000000000002, 'MSZoning_1'), (0.0080000000000000002, 'Foundation_3'), (0.0070000000000000001, 'Neighborhood_5'), (0.0070000000000000001, 'BsmtFinType1_0'), (0.0060000000000000001, 'HouseStyle_1'), (0.0060000000000000001, 'ExterQual_1'), (0.0050000000000000001, 'LandContour_0'), (0.0050000000000000001, 'HouseStyle_6'), (0.0050000000000000001, 'BsmtFinType1_1'), (0.0050000000000000001, 'BsmtCond_1'), (0.0040000000000000001, 'Neighborhood_18'), (0.0040000000000000001, 'ExterCond_1'), (0.0030000000000000001, 'Exterior2nd_10'), (0.0030000000000000001, 'BldgType_1'), (0.002, 'Street_0'), (0.002, 'SaleCondition_1'), (0.002, 'Heating_3'), (0.002, 'Functional_3'), (0.002, 'Functional_1'), (0.002, 'BsmtExposure_3'), (0.001, 'SaleType_0'), (0.001, 'MSZoning_2'), (0.001, 'LandContour_1'), (0.001, 'Condition1_5'), (0.001, 'BsmtExposure_0'), (-0.0, 'Neighborhood_20'), (0.0, 'Exterior2nd_7'), (0.0, 'Exterior2nd_6'), (-0.0, 'Exterior2nd_2'), (-0.0, 'Exterior1st_7'), (-0.0, 'Exterior1st_1'), (0.0, 'BsmtFinType2_5'), (-0.0, 'BsmtCond_3'), (0.0, 'BldgType_3'), (-0.001, 'SaleType_1'), (-0.001, 'SaleCondition_2'), (-0.001, 'Neighborhood_6'), (-0.001, 'Neighborhood_0'), (-0.001, 'LotConfig_3'), (-0.001, 'LandContour_2'), (-0.001, 'Heating_0'), (-0.001, 'Functional_5'), (-0.001, 'Exterior2nd_9'), (-0.001, 'Exterior2nd_4'), (-0.001, 'Exterior1st_6'), (-0.001, 'Exterior1st_4'), (-0.001, 'Condition2_3'), (-0.001, 'Condition2_0'), (-0.001, 'Condition1_4'), (-0.002, 'Utilities_0'), (-0.002, 'RoofStyle_4'), (-0.002, 'RoofMatl_2'), (-0.002, 'Neighborhood_2'), (-0.002, 'MasVnrType_0'), (-0.002, 'HouseStyle_4'), (-0.002, 'Heating_4'), (-0.002, 'Functional_4'), (-0.002, 'Functional_2'), (-0.002, 'Foundation_4'), (-0.002, 'Exterior2nd_1'), (-0.002, 'ExterCond_3'), (-0.002, 'Electrical_3'), (-0.002, 'Electrical_2'), (-0.002, 'Condition1_6'), (-0.002, 'BsmtFinType2_1'), (-0.0030000000000000001, 'SaleType_5'), (-0.0030000000000000001, 'SaleType_3'), (-0.0030000000000000001, 'RoofStyle_0'), (-0.0030000000000000001, 'RoofMatl_5'), (-0.0030000000000000001, 'RoofMatl_3'), (-0.0030000000000000001, 'RoofMatl_1'), (-0.0030000000000000001, 'RoofMatl_0'), (-0.0030000000000000001, 'Neighborhood_14'), (-0.0030000000000000001, 'MiscVal'), (-0.0030000000000000001, 'MasVnrArea'), (-0.0030000000000000001, 'LowQualFinSF'), (-0.0030000000000000001, 'Exterior2nd_3'), (-0.0030000000000000001, 'Condition2_5'), (-0.0040000000000000001, 'SaleType_7'), (-0.0040000000000000001, 'RoofStyle_2'), (-0.0040000000000000001, 'Neighborhood_1'), (-0.0040000000000000001, 'Heating_1'), (-0.0040000000000000001, 'HeatingQC_3'), (-0.0040000000000000001, 'Exterior2nd_11'), (-0.0040000000000000001, 'Exterior1st_9'), (-0.0040000000000000001, 'Exterior1st_3'), (-0.0040000000000000001, 'Exterior1st_2'), (-0.0040000000000000001, 'Condition2_1'), (-0.0040000000000000001, 'BsmtHalfBath'), (-0.0040000000000000001, 'BsmtFinType2_0'), (-0.0050000000000000001, 'SaleType_2'), (-0.0050000000000000001, 'RoofMatl_4'), (-0.0050000000000000001, 'Neighborhood_8'), (-0.0050000000000000001, 'Neighborhood_11'), (-0.0050000000000000001, 'LotShape_2'), (-0.0050000000000000001, 'LotConfig_2'), (-0.0050000000000000001, 'Exterior1st_10'), (-0.0050000000000000001, 'Condition2_6'), (-0.0060000000000000001, 'RoofMatl_6'), (-0.0060000000000000001, 'LotConfig_0'), (-0.0060000000000000001, 'LandSlope_0'), (-0.0060000000000000001, 'Exterior2nd_12'), (-0.0060000000000000001, 'Exterior1st_11'), (-0.0060000000000000001, 'Electrical_4'), (-0.0070000000000000001, 'PavedDrive_1'), (-0.0070000000000000001, 'Neighborhood_4'), (-0.0070000000000000001, 'Neighborhood_13'), (-0.0070000000000000001, 'ExterCond_0'), (-0.0070000000000000001, 'Condition2_2'), (-0.0070000000000000001, 'BsmtFinType2_3'), (-0.0070000000000000001, 'BsmtFinType2_2'), (-0.0070000000000000001, 'BsmtFinSF2'), (-0.0080000000000000002, 'SaleCondition_3'), (-0.0080000000000000002, 'HouseStyle_2'), (-0.0080000000000000002, 'Functional_0'), (-0.0080000000000000002, 'Exterior1st_5'), (-0.0080000000000000002, 'Condition1_7'), (-0.0080000000000000002, 'Condition1_3'), (-0.0089999999999999993, 'Condition2_4'), (-0.01, 'HouseStyle_3'), (-0.01, 'Heating_2'), (-0.010999999999999999, 'MasVnrType_2'), (-0.010999999999999999, 'ExterCond_2'), (-0.012, 'PoolArea'), (-0.016, 'YrSold'), (-0.016, 'ScreenPorch'), (-0.017999999999999999, '3SsnPorch'), (-0.019, 'LandSlope_1'), (-0.025000000000000001, 'SaleType_4'), (-0.027, 'MoSold'), (-0.036999999999999998, 'Id')]

Die Bewertung unserer Merkmale findet durch den Bestimmtheitsmaß R² statt.

Als Top-Features erkennbar sind folgende Merkmale:

OverallQual
GrLivArea
GarageCars
TotalBsmtSF
GarageArea
1stFlrSF
FullBath
YearBuilt

Schauen wir in unsere Heatmap erkennen wir viele Merkmale wieder. Ob uns das wundern sollte? Ich denke nicht. Wir sehen, beide Verfahren eignen sich ziemlich gut, um starke und schwache Merkmale zu identifizieren.

Tareq Haschemi

A man who works with data